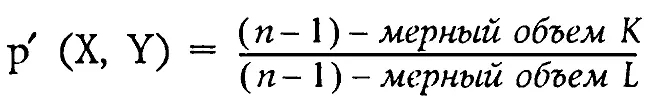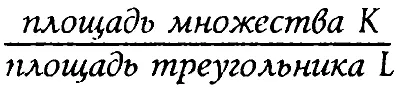Анатолий Фоменко - Истину можно вычислить.

Наконец, вспомним, что при подсчете коэффициента р''(X, Y) летописи X и Y оказались в неравноправном положении. Дело в том, что выше мы рассматривали «n-мерный шар» радиуса r(X, Y) с центром в точке а(X). Чтобы устранить возникшее неравноправие между летописями X и Y, просто поменяем их местами и повторим описанную выше конструкцию, взяв теперь за центр «n-мерного шара» точку a(Y). В результате получится некоторое число, которое мы обозначим через p''(Y, X). В качестве «симметричного коэффициента» p(X, Y) мы возьмем среднее арифметическое чисел р''(X, Y) и p''(Y,X), то есть

½ (р''(X, Y) + p''(Y, X)).

Для наглядности поясним смысл предварительного коэффициента р'(X, Y) на примере графиков объема всего лишь с двумя локальными максимумами. В этом случае оба вектора

а(X) = (х 1, x 2, х 3) и a(Y) = (у 1, у 2, у 3)

являются векторами в трехмерном евклидовом пространстве. Концы этих векторов лежат на двумерном равностороннем треугольнике L, отсекающем от координатных осей в пространстве R 3одно и то же число В — А. Рис. 8. Если расстояние от точки а(X) до точки а(Y) обозначить через |а(X) — а(Y)|, то множество К — это пересечение треугольника L с трехмерным шаром, центр которого находится в точке а(X), а радиус равен |а(X) — а(Y)|. После этого нужно подсчитать количество «целых точек», то есть точек с целочисленными координатами, в множестве К и в треугольнике L. Взяв отношение получившихся чисел, мы и получим коэффициент р'(X, Y).

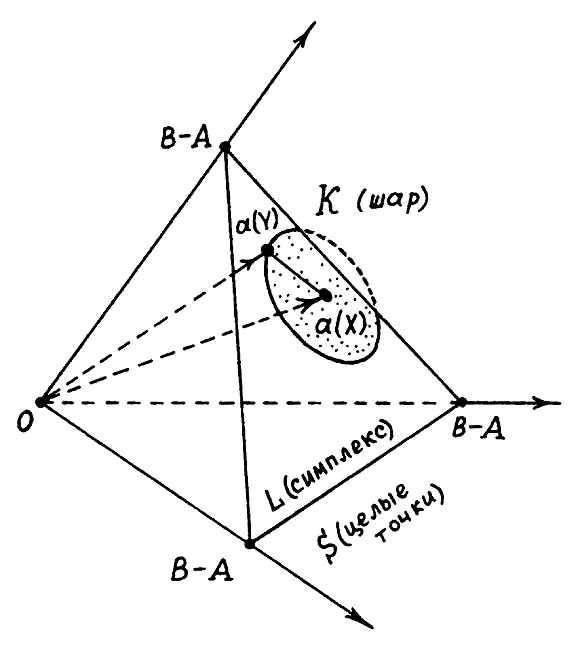
Рис. 8. Векторы а(X) и а(Y) определяют «шар», часть которого попадает в симплекс L.

При конкретных вычислениях удобно пользоваться приближенным способом вычисления коэффициента p(X, Y). Дело в том, что подсчет числа целых точек в множестве К довольно затруднителен. Но оказывается, эту трудность можно обойти, перейдя от «дискретной модели» к «непрерывной модели». Хорошо известно, что если (n-1)-мерное множество К в (n-1)-мерном симплексе L достаточно велико, то число целых точек в К примерно равно (n-1)-мерному объему множества К. Поэтому с самого начала в качестве предварительного коэффициента р'(X, Y) можно брать просто отношение (n-1)-мерного объема K к (n-1)-мерному объему L, то есть

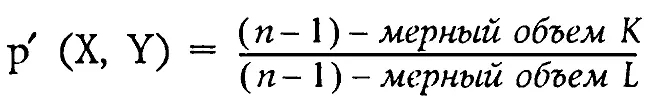
Например, в случае двух локальных максимумов в качестве коэффициента р'(X, Y) следует взять отношение

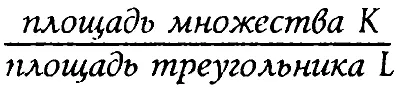
Конечно, при малых значениях В — А «дискретный коэффициент» и «непрерывный коэффициент» различны. Но в наших исследованиях мы будем иметь дело с временны́ми интервалами В — А в несколько десятков и даже сотен лет, так что для интересующих нас целей можно, не делая большой ошибки, уверенно пользоваться «непрерывной моделью» р'(X, Y). Точные математические формулы для подсчета «непрерывного коэффициента» р'(X, Y), для его оценки сверху и снизу, приведены в работе [884], с. 107.

Укажем еще одно уточнение описанной статистической модели. При работе с конкретными графиками объема исторических текстов следует «сглаживать» эти графики, чтобы устранить мелкие случайные всплески. Мы проводили такое сглаживание графика, «усредняя по соседям», то есть, заменяя значение функции объема в каждой точке t на среднее арифметическое трех значений функции, а именно в точках t — 1, t, t + 1.В качестве «окончательного коэффициента» p(X, Y) следует взять его значение, подсчитанное для таких «сглаженных графиков».

Сформулированный выше принцип корреляции максимумов подтвердится, если для большинства пар заведомо зависимых текстов X и Y коэффициент p(X, Y) окажется «малым», а для большинства пар заведомо независимых текстов, напротив, — «большим».

В 1978–1985 годах автором был проведен первый обширный вычислительный эксперимент по подсчету чисел p(X, Y) для нескольких десятков пар конкретных исторических текстов-хроник, летописей и т. п. Детали см. в [904], [908], [1137], [884].

Оказалось, что коэффициент p(X, Y) достаточно хорошо различает ЗАВЕДОМО ЗАВИСИМЫЕ и ЗАВЕДОМО НЕЗАВИСИМЫЕ пары исторических текстов. Было обнаружено, что для всех исследованных нами пар реальных летописей X, Y, описывающих ЗАВЕДОМО РАЗНЫЕ события (разные исторические эпохи или разные государства), то есть для НЕЗАВИСИМЫХ текстов, число p(X, Y) колеблется от 1 до 1/100 при количестве локальных максимумов от 10 до 15. Напротив, если исторические летописи X и Y ЗАВЕДОМО ЗАВИСИМЫ, то есть описывают одни и те же события, то число p(X, Y) не превосходит 10 -8для того же количества максимумов.