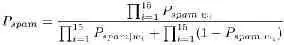Paul Graham - Hackers and Painters - Big Ideas from the Computer Age

Here's a sketch of how I do statistical filtering. I start with one corpus of spam and one of non spam mail. At the moment each one has about 4000 messages in it. I scan the entire text, including headers and embedded HTML and Javascript, of each message in each corpus. I currently consider alphanumeric characters, dashes, apostrophes, and dollar signs to be part of tokens, and everything else to be a token separator. (There is probably room for improvement here.) I ignore tokens that are all digits, and I also ignore HTML comments, not even considering them as token separators.

I count the number of times each token (ignoring case, currently) occurs in each corpus. At this stage I end up with two large hash tables, one for each corpus, mapping tokens to number of occurrences.

Next I create a third hash table, this time mapping each token to the probability that an email containing it is a spam, Pspam|w which I calculate as follows:

r g = min (1, 2(good (w)/G)), rb = min (1, bad (w)/B)

Pspam|w = max(.01,min (.99, rb /( rg + rb )))

where w is the token whose probability we're calculating, good and bad are the hash tables I created in the first step, and G and B are the number of non spam and spam messages respectively.

I want to bias the probabilities slightly to avoid false positives, and by trial and error I've found that a good way to do it is to double all the numbers in good. This helps to distinguish between words that occasionally do occur in legitimate email and words that almost never do. I only consider words that occur more than five times in total (actually, because of the doubling, occurring three times in non spam mail would be enough). And then there is the question of what probability to assign to words that occur in one corpus but not the other. Again by trial and error I chose .01 and .99. There may be room for tuning here, but as the corpus grows such tuning will happen automatically anyway.

The especially observant will notice that while I consider each corpus to be a single long stream of text for purposes of counting occurrences, I use the number of emails in each, rather than their combined length, as the divisor in calculating spam probabilities. This adds another slight bias to protect against false positives.

When new mail arrives, it is scanned into tokens, and the most interesting fifteen tokens, where interesting is measured by how far their spam probability is from a neutral .5, are used to calculate the probability that the mail is spam. If w1, . . . , w15 are the fifteen most interesting tokens, you calculate the combined probability thus:

Figure 8-1.

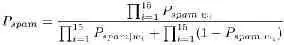
One question that arises in practice is what probability to assign to a word you've never seen, i.e. one that doesn't occur in the hash table of word probabilities. I've found, again by trial and error, that .4 is a good number to use. If you've never seen a word before, it is probably fairly innocent; spam words tend to be all too familiar.

I treat mail as spam if the algorithm above gives it a probability of more than .9 of being spam. But in practice it would not matter much where I put this threshold, because few probabilities end up in the middle of the range.

One great advantage of the statistical approach is that you don't have to read so many spams. Over the past six months, I've read literally thousands of spams, and it is really kind of demoralizing. Norbert Wiener said if you compete with slaves you become a slave, and there is something similarly degrading about competing with spammers. To recognize individual spam features you have to try to get into the mind of the spammer, and frankly I want to spend as little time inside the minds of spammers as possible.

But the real advantage of the Bayesian approach, of course, is that you know what you're measuring. Feature-recognizing filters like Spam Assassin assign a spam "score" to email. The Bayesian approach assigns an actual probability. The problem with a "score" is that no one knows what it means. The user doesn't know what it means, but worse still, neither does the developer of the filter. How many points should an email get for having the word sex in it? A probability can of course be mistaken, but there is little ambiguity about what it means, or how evidence should be combined to calculate it. Based on my corpus, sex indicates a .97 probability of the containing email being a spam, whereas sexy indicates .99 probability. And Bayes's Rule, equally unambiguous, says that an email containing both words would, in the (unlikely) absence of any other evidence, have a 99.97% chance of being a spam.

Because it is measuring probabilities, the Bayesian approach considers all the evidence in the email, both good and bad. Words that occur disproportionately rarely in spam (like though or tonight or apparently) contribute as much to decreasing the probability as bad words like unsubscribe and opt-in do to increasing it. So an otherwise innocent email that happens to include the word sex is not going to get tagged as spam.

Ideally, of course, the probabilities should be calculated individually for each user. I get a lot of email containing the word Lisp, and (so far) no spam that does. So a word like that is effectively a kind of password for sending mail to me. In my earlier spam-filtering software, the user could set up a list of such words and mail containing them would automatically get past the filters. On my list I put words like Lisp and also my zipcode, so that (otherwise rather spammy-sounding) receipts from online orders would get through. I thought I was being very clever, but I found that the Bayesian filter did the same thing for me, and moreover discovered of a lot of words I hadn't thought of.

When I said at the start that our filters let through less than 5 spams per 1000 with 0 false positives, I'm talking about filtering my mail based on a corpus of my mail. But these numbers are not misleading, because that is the approach I'm advocating: filter each user's mail based on the spam and non spam mail he receives. Essentially, each user should have two delete buttons, ordinary delete and delete-as-spam. Anything deleted as spam goes into the spam corpus, and everything else goes into the non spam corpus.

You could start users with a seed filter, but ultimately each user should have his own per-word probabilities based on the actual mail he receives. This (a) makes the filters more effective, (b) lets each user decide their own precise definition of spam, and (c) perhaps best of all makes it hard for spammers to tune mails to get through the filters. If a lot of the brain of the filter is in the individual databases, then merely tuning spams to get through the seed filters won't guarantee anything about how well they'll get through individual users' varying and much more trained filters.

Content-based spam filtering is often combined with a white list, a list of senders whose mail can be accepted with no filtering. One easy way to build such a white list is to keep a list of every address the user has ever sent mail to. If a mail reader has a delete as spam button then you could also add the from address of every email the user has deleted as ordinary trash.

I'm an advocate of white lists, but more as a way to save computation than as a way to improve filtering. I used to think that white lists would make filtering easier, because you'd only have to filter email from people you'd never heard from, and someone sending you mail for the first time is constrained by convention in what they can say to you. Someone you already know might send you an email talking about sex, but someone sending you mail for the first time would not be likely to. The problem is, people can have more than one email address, so a new from address doesn't guarantee that the sender is writing to you for the first time. It is not unusual for an old friend (especially if he is a hacker) to suddenly send you an email with a new from-address, so you can't risk false positives by filtering mail from unknown addresses especially stringently.