Андрей Битов - Пятое измерение. На границе времени и пространства (сборник)

Ну, что я могу сказать? Некоторые мои личные ощущения совпадают… Тот факт, что в Золотом веке напротив Пушкина нет никого, ни одного знаменитого писателя или поэта, говорит о том, что в Золотом веке нет ни одного продолжателя Пушкина (реального). В следующем веке это кто? – Вл. Соловьев и Ахматова, Волошин. На самом деле и они не являются продолжателями всего того, что заложено Пушкиным. На самом деле до сих пор нет реально ни одного продолжателя Пушкина. Нет такого яркого выражения продолжения, как Толстой – Солженицын. Или такой наглядности, как в год Змеи, который для России как будто выражает кармический цикл: что заложено в глубине души, все подсознание, все кризисы, скрытые, задавленные… Пушкин, конечно, занимает особое место. Не помещается в отведенную ему ячейку. Он как бы покрывает собой и весь цикл, и все циклы. Самое удивительное в том, что представил Битов, для меня как раз не цикличность, не последовательные взаимосвязи, а этот единый замысел русской литературы, все похоже на единый процесс построения некоего здания. Это часто бывает, что много циклов проходит, прежде чем появится плод из брошенного в почву семени. Справедливо считается, что очень глубокие проявления выявляются через много циклов. Как раз по поводу Пушкина мне вспомнилась идея краеугольного камня. Приведу пример, заимствованный мной из одной мистической книги. При построении пирамиды древними самый последний камень, который клали на вершину пирамиды, делался в самом начале и откладывался в сторону. А когда строительство всего здания завершалось, его поднимали наверх. Исходя из этой аналогии, у Пушкина не только нет продолжателей, но и не будет, а когда завершится здание российской литературы, последней ступенью в этой литературе станет Пушкин. То есть Пушкин – завершение или образ завершения, а не начал. Конечно, начало тоже, но в виде пика.

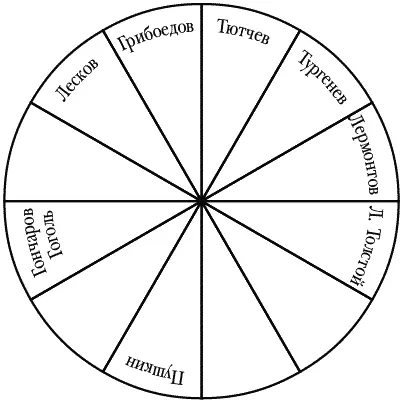
А. Г. БИТОВ (разглядывая круги Левина) : Слишком густо… Тут уже мало что можно сказать… Разве что Лермонтов по-прежнему относительно одинок, а Петух – сравнительно бедноват. Может, Петух – как раз и есть будущий русский писатель? Может, он как раз сегодня родился? Надо бы отдельно построить и XVIII век, до Золотого. И поэзию отдельно от прозы… То, что верно в начале литературы, потом верно лишь в отношении поколений, а потом… чем плотнее прошлое, тем беднее картина настоящего. Что же касается зодиаков, то тут я уж совсем не берусь рассуждать… Почему Весы родят поэтов (вот где Лермонтов не одинок…), почему так много Водолеев и так мало Рыб и Тельцов? Признаться, цель у меня была достаточно утилитарная – почистить литературный календарь от партийной патины. Не юбилеем и даже не зодиаком награждать писателя, а его именем награждать месяц: скажем, май-Булгаков, июнь-Пушкин… Впрочем, не получится: припахивает не то Французской, не то Октябрьской революцией (с литературным уклоном)… Попробуем хотя бы расписать наш первый (Золотой) круг и по зодиаку. Это что же получается?! Что они не только в своего зверя метили, но и в свой знак?! И так были разные, и опять разные? Великий русский писатель удостаивается персональной звезды…

Не слишком ли? Что-то слишком уж получается. Подозрительно. Собирался еще одним простодушным способом описать историю русской литературы, а выступил апологетом астрологии… Надо бы с математиком проконсультироваться… Число сочетаний из всех… по одному… по единственному… Если у нас 12 x 12 = 144 варианта звездных рождений… то не каждый ли человек будет одинешенек в толпе из 143 человек? Но с другой стороны, отнюдь не на 144 человека приходится один великий писатель… Какова вероятность не повториться? Да ведь точно, что несравнима как раз с вероятностью повториться. И каждый окажется чемпион в цепи случайностей, и только победа закономерна? И не Близнец-Овца, а Пушкин. И не Собака-Весы, а Лермонтов… «…И не был // убийцею создатель Ватикана?»

Р. S.Случай свел меня в 1996 году в Принстоне с математиком Е. Гурием, посещавшим мой семинар по Пушкину. Я попросил его описать на языке самой точной из наук столь редкостные звездные сгущения русских поэтов Золотого и Серебряного веков. Изучив мой текст, он выписал следующее членистоногое уравнение: