Ральф Рене - Как NASA показало Америке Луну

Даже если бы было два Солнца, ни одно из них не могло в момент съемки располагаться в 10 град. над горизонтом! Простейших знаний в области тригонометрии достаточно, чтобы произвести вычисления: персональный источник освещения Олдрина находится на высоте, равной:

a tan (5,588 / 11,277) = a tan (0,496) = 26,4 град.,

а Армстронга — на высоте, равной:

a tan (5,436 / 7,785) = a tan (0,698) = 34,9 град.

Выход из корабля произошел через 7 часов после прилунения. Поскольку лунный день длится 30 земных дней, Солнце движется через лунное небо со скоростью 12 град. в 24 часа. Семь часов соответствуют 3,5 град., значит, во время знаменитой космической прогулки Солнце было бы на высоте 13,5 град. над горизонтом.

При такой высоте Солнца длина теней на изображении должна составлять более 23 см, то есть в два с лишним раза длиннее того, что видно на фото! Единственный источник света не может отбрасывать настолько разные тени от людей почти одного роста. И, как справедливо заметил мистер Карто, хотелось бы понять, где тень от флага, которая должна «разрезать» Армстронга пополам?

В NASA объяснили наличие удлиненной тени тем, что тень флага якобы добавляется к тени астронавта. Но внимательный анализ фотографии разбивает и этот довод: хорошо видно, что тень древка упирается в ногу Армстронга, а самый верх тени флага выходит из «макушки» тени астронавта, поэтому тень флага никак не может добавляться к тени Олдрина. Как ни крути, снимок явно сфабрикован!

Люди, прочитавшие «Следы на Луне», нашли еще множество несоответствий в фотографиях NASA. Мне рассказывали, что после сканирования некоторых цветных фотографий фоновые пятна в определенных местах принимают другой оттенок, что характеризует «составную» фотографию, сделанную из снимков с разных типов пленок. Я не стал добавлять эти замечания к тексту, дабы не лишать читателя возможности самостоятельно найти дополнительные несоответствия.

В октябре 1995 я решил исследовать фотографии Аполлонов на предмет длины теней и их соотношения с местоположением и углом возвышения Солнца в соответствующие дни и время. Требовалось вычислить угол возвышения Солнца над лунным горизонтом, чтобы определить длину тени на тот момент времени, когда астронавты прогуливались по Луне. Мне надо было лишь освежить свои знания в области сферической тригонометрии и астронавигации.

Я пошел в местную библиотеку — проштудировать справочники и записать формулы, необходимые для измерения углов возвышения Солнца во время каждой из предполагаемых лунных посадок и взлетов. Точное время новолуния перед каждой из миссий «Аполлона» определит путь Луны с этого мгновения до посадки и взлета. Поскольку миссии исчислялись с момента пуска с Земли, мне нужно было знать точное время запуска, а также широту и долготу мест посадки на Луне.

С изумлением я обнаружил, что в источниках указаны разные данные о координатах и времени посадки. NASA, которое всегда кичилось своей пунктуальностью, не могло точно записать время и зафиксировать координаты! Для двух миссий время вообще не было указано, но мне удалось его вычислить с погрешностью в несколько часов. Я написал в NASA — мне было интересно, что они скажут по этому поводу, но на ответ я особо не рассчитывал: если NASA решит следовать выбранному пути, ответа мне не дождаться никогда. А пока суть да дело, я использовал те координаты и время, которые мне удалось найти.

Точные астрономические данные о времени новолуния перед каждой миссией я взял в соответствующем морском справочнике. Физико-химический справочник подсказал мне наклон полярной оси и орбиты Луны. Наклон оси составляет 1,537 град., а орбиты — 5,12 град. к плоскости эклиптики. Там же я нашел данные о периоде обращения Луны вокруг своей оси — 2 360 550 секунд, или 27,32 дней. Это означает, что за один земной день Луна проходит 13,176 град.

Ниже приведены данные по миссиям. В каждой таблице последние два столбца первой строки — это количество часов с момента запуска с Земли до прилунения и до обратного старта с Луны соответственно. Во второй строке указаны дата и время предшествовавшего запуску новолуния и количество дней и часов до прилунения и обратного старта соответственно. Третья строка показывает суммарное количество дней и часов от новолуния до старта, в четвертой строке — количество часов от новолуния до прилунения и обратного старта, а в пятой — количество часов оборота с момента новолуния.

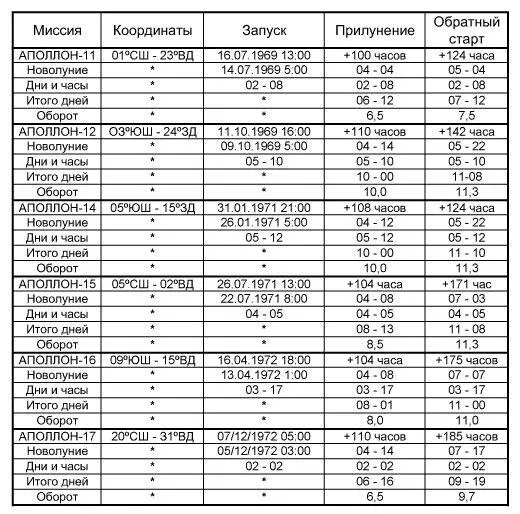
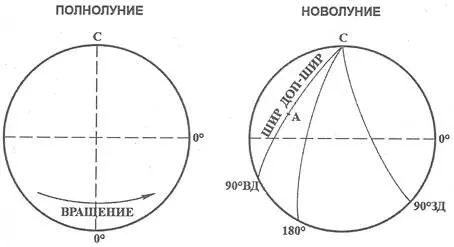
Рис. 15. Слева: полнолуние, справа: новолуние