Иван Иванович Иванов (его главный секретный псевдоним) именно в таком ключе и рассматривал систему наказаний в Гулаге.
Понятно, что все атеисты – грешники изначально.
А потому любой наказываемый изначально за свой атеизм и получал честно заработанную «десятку».
Это как бы минимальный срок поста.
Беременная женщина в таком случае – это всем прочим грешницам грешница!
Поверить в непорочное зачатие атеистки не было ни малейшей возможности.
Оставалось одно: терпеть и молиться.
В то же время, будучи человеком глубоко криминальным он учил своих учеников примерно таким образом:
– Делайте, что хотите, но не оставляйте следов!
Главный конструктор Гулага любил, по некоторым слухам, разведку, общался с настоящими мастерами этого дела, ценил добывание и обработку.
Воспитанный великими умельцами прятания концов в воду, наиконспиративнейшими конспираторами из всех конспираторов, он не строил иллюзий.
Он скрывал следы.
Уничтожал даже намек на информацию о себе самом и о своих достижениях.
А задача стояла нетривиальная.
С одной стороны империю нужно было держать в повиновении, а без хорошо поставленной обратной связи управлять столь сложным организмом затруднительно.
С другой стороны оставление следов есть само по себе покушение на него и его принципы.
И вот рождается удивительнейшая система искажения информации, включающая в себя и ключи доступа к информации объективной и достоверной.
Приведу один пример из практики расстрела моего деда.
В 1956-ом году семье сообщили заведомо ложную информацию о дате его гибели.
По справке от государства мой дед умер 13 -го ноября 1941 года.
В 1991 году семья получила от государства справку, что дед был расстрелян 13 мая 1938 года!
И вот здесь вскрылось вдруг для меня, как именно информация будучи искажаемой сохранялась. К году смерти тупо прибавляли ТРИ, к дате смерти тупо добавляли ШЕСТЬ МЕСЯЦЕВ!!! И глядя на ложный документ человек владеющий этой отмычкой мог легко вычислить реальную дату расстрела!
И вот глядя на эти пропуски в данных и повторяющиеся странным образом цифры я пытаюсь понять: какой же тут КЛЮЧ?
Ведь он здесь точно присутствует!!!
Ведь надо понимать генералиссимуса и его ходы.
Иначе не прочесть нам и строки в этой странноватой жуткой Книге Смерти.
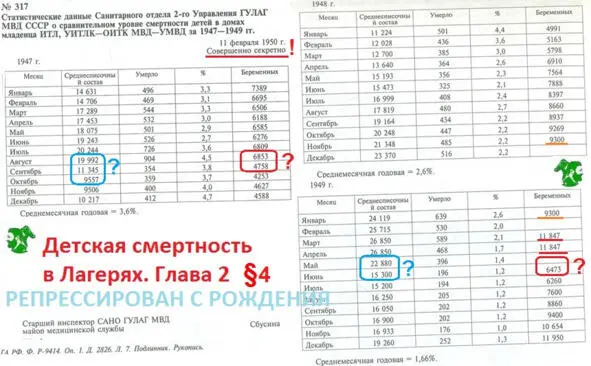
Детская смертность в лагерях. Глава вторая 4
Одиннадцать тысяч беременных в державе.
Много это или мало?
Предположим чисто теоретически, что население державы равно 216 миллионам человек.
Откель цифирка?
С потолка!
Почему такая?
Вот сейчас построим «мудрель» то бишь модель, и сразу станет понятно.
Предположим далее, что средний возраст жизни в державе 72 года.
Опять цифирка с потолка.
Но нам так удобнее будет считать.
Итак: при сохранении численности неизменной необходимо, чтобы за 72 года население полноценно обновилось.
Делим 216 на 72 и получаем ровно три!
То есть ежегодно в державе должно рожаться ТРИ МИЛЛИОНА граждан!
То есть ежедневно должны рождаться 3 000 000 / 365 = 8220 человек!
Но не все беременности бывают удачными, не все роды заканчиваются живорожденностью.
Потому мы сию цифирку нашу среднепотолочную простенько округлим до 9000!
То есть 9000 беременных ежедневно должны разрешаться от бремени, дабы страна с населением в 216 миллионов при средней продолжительности жизни в 72 года могла иметь стабильное пребывание в мире.
Ну а если население 180 миллионов, а продолжительность жизни 60 лет?
Точно те же самые три миллиона в год и все те же 9000 ежесуточно!
Вот у нас примерно с такими «параметрами» страна и оказалась.
То есть в лагерях пребывала примерно суточная доза рожающих всей страны.
Проще говоря одна 270-я доля всех беременных.
А что это за цифирка?
А это средний срок длительности одной беременности в сутках.
Чтобы 9000 беременных могли рожать ежесуточно, требуется иметь 2 миллиона 430 тысяч беременных одновременно!
А это одна семьдесят четвёртая часть ставосьмидесятимиллионного населения!
То есть одна из 37 женщин при условии равенства полов должна быть непременно беременна!
Опять же для ровного счета представим себе, что одна из 36 при 72 годах продолжительности жизни.
То есть из 72 женщин беременными непрерывно должны быть две.
Читать дальше