Ответ. 889.
Д55. Какие выводы можно сделать из первой фразы А? Во-первых, известное ему произведение P не является произведением двух простых чисел p 1и p 2(иначе разложение 1 · p 1· p 2было бы единственным). Во-вторых, если произведение трех различных натуральных чисел не превосходит 50, то их сумма не превосходит 1 + 2 + 25 = 28. А раз число, которое сообщили математику А, могло бы быть и суммой трех чисел, оно не больше 28. С другой стороны, Р не меньше 21. Действительно, если бы Р было меньше 21, то были бы возможны как минимум два варианта троек чисел с суммой Р: 1 + 2 + (Р – 3) (произведение не больше 1. 2.17 = 34) и 1 Н -3 (Р – 4) (произведение не больше 1-3-16 = 48).
Есть только два числа, соответствующие первой фразе А: 24 и 28.
24 = 1– 2-12 = 1– 3–8 = 1– 4–6 = 2– 3–4 (суммы соответственно 15, 12, 11 и 9);
28 = 1– 2-14 = 1– 4–7 (суммы соответственно 17 и 12).
Ответ Б «Я все равно не знаю их» означает, что известная ему сумма встречается среди этих вариантов более одного раза, т. е. равна 12. Если А сообщили число 24, то он сделает вывод, что задуманы числа 1, 3 и 8. А если ему сообщили число 28, то он поймет, что задуманы числа 1, 4 и 7.
Д56. Зная номера троих других а < b < с, математик понимает, что его номер равен либо а + b + с, либо с – а – b. Раз математик не смог определить свой номер, оба этих выражения должны давать двузначное число (то есть лежать в пределах от 10 до 99) и не совпадать с другими номерами.
Пусть 10 ≤ x < y < z < t ≤ 99—искомые номера, тогда t = x + y + z. Поскольку математик с номером t знает числа x < y < z, число z − x − y двузначно и отлично от x и y. Но тогда z = x + y + (z − x − y) ≥ 10 + 11 + 12 = 33. Заметим еще, что t = z + y + x ≥ z + 11 + 10, то есть t ≥ z + 21. Математик с номером x знает числа y < z < t, значит, y + z + t ≤ 99. Сложив это неравенство с неравенствами 11 ≤ y и z + 21 ≤ t, получим 2z ≤ 67, откуда z ≤ 33. Значит, z = 33. Далее, t = x + y + z > 10 + y + 33 = 43 + y, поэтому 99 > y + z + t > y + 33 + (43 + y) = 76 + 2y. Отсюда 2y ≤ 23, то есть y ≤ 11. Значит, y = 11, x = 10, z = 33 и t = 10 + 11 + 23 = 54. Нетрудно убедиться, что этот набор удовлетворяет условию.
Ответ.10, 11, 33 и 54.
Д57.Пусть x, y, z – числа, написанные на лбу первого, второго и третьего логика соответственно.
Вначале с точки зрения первого логика возможны варианты x = y + z и x = |y − z|. Поэтому первый логик сможет догадаться, какое у него число, только если y = z. Значит, после первого высказывания все знают, что y ≠ z.
Теперь с точки зрения второго логика возможны такие варианты: y = x + z и y = |x − z|, причем y ≠ z. Поэтому второй логик сможет догадаться, какое у него число, только если x = z или x = 2z. Значит, после второго высказывания все знают, что x ≠ z и x ≠ 2z.
Тогда с точки зрения третьего логика возможны такие варианты: z = x + y и z = |x − y|, причем z не равно ни одному из чисел y, x или x/2. Поэтому третий логик сможет догадаться, какое у него число, только если x 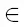 {y, 2y, y/2, 2y/3}. Значит, после третьего высказывания все знают, что x
{y, 2y, y/2, 2y/3}. Значит, после третьего высказывания все знают, что x 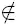 {y, 2y, y/2, 2y/3}.
{y, 2y, y/2, 2y/3}.
Теперь с точки зрения первого логика возможны варианты x = y + z и x = |y − z|. При этом известно, что x /2 {y, 2y, y/2, 2y/3, z, 2z} и y ≠ z. Поэтому первый логик сможет догадаться, какое у него число, только если y + z или |y − z| равно одному из чисел y, 2y, y/2, 2y/3, z, 2z и y ≠ z. Это возможно, только если y − z равно одному из чисел y/2, 2y/3, z, 2z, −y, −2y, −y/2, −2y/3. В этих случаях x = y + z и равно 3y/2, 4y/3, 3z, 4z, 3y, 4y, 5y/2, 8y/3 соответственно. Поскольку 50 не делится ни на 3, ни на 4, то имеет место случай x = 5y/2. Тогда y = 20, z = 30.
Ответ.У второго 20, у третьего 30.
Заметная часть вошедших в этот выпуск задач являются по сути техническими упражнениями, придуманными специально для данного занятия. Другие, напротив, так давно вошли в математический фольклор, что их авторство установить затруднительно. Ниже указаны известные нам авторы задач, позаимствованных из классической литературы и математических соревнований.
М. Гарднер: 7.12.
А. В. Грибалко: 7.13.
С. В. Грибок: Д54.
К. А. Кноп: 10.12, Д52, Д55.
А. Н. Печковский: 7.14.
И. В. Раскина: 4.18, 9.11.
A. И. Сгибнев Д43.
Р. М. Смаллиан: 4.13, 4.14, 4.15, 9.5, 9.6.
B. А. Уфнаровский, А. Я. Канель-Белов: Д36.
Б. Р. Френкин: Д35.
А. С. Чеботарев: Д39.
А. В. Шаповалов: 8.10, 9.10, Д44, Д46, Д47, Д56, Д57.
Д. Э. Шноль: 9.3, 9.8, Д43.
1. Р. М. Смаллиан. Как же называется эта книга? – М.: Издательский дом Мещерякова, 2008.
2. Р. М. Смаллиан. Принцесса или тигр? – М.: Мир, 1985.
3. Л. Кэрролл. Логическая игра. – М.: Наука, 1991.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

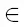 {y, 2y, y/2, 2y/3}. Значит, после третьего высказывания все знают, что x
{y, 2y, y/2, 2y/3}. Значит, после третьего высказывания все знают, что x 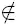 {y, 2y, y/2, 2y/3}.
{y, 2y, y/2, 2y/3}.








