Инесса Раскина - Логика для всех. От пиратов до мудрецов

Таким образом, возможны три неразличимых варианта: нет умных, один уверенный умный и два скромных умных. Во всех этих случаях все участники опроса ответят: «Один».

Посмотрим, какие ответы даст опоздавший думец в каждой из этих ситуаций в зависимости от его ума и скромности:

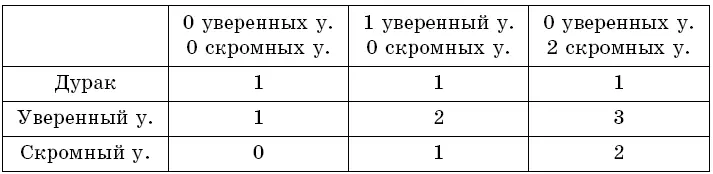
Видно, что ответы «1» и «2» встречаются в нескольких клетках, т. е. такие ответы не помогли бы различить ситуации. Зато ответы «О» и «3» встречаются в таблице по одному разу и позволяют сделать однозначный вывод. Значит, опоздавший дал один из этих ответов. В первом случае в думе один умный, во втором – три.

Ответ.1 или 3.

Д44. 1) Занумеруем карты от 0 до 6. Можно считать, что у Гриши карты 1, 2 и 3. Пусть он скажет: «У меня либо набор 1, 2, 3, либо набор 4, 5, 6». Поскольку у Леши на руках как минимум две карты из набора 4, 5, 6, он понимает, что у Гриши набор 1, 2, 3, и знает, какая карта спрятана. Теперь Леша должен сообщить Грише свои карты. Возможны два случая.

1. У Леши набор 4, 5, 6 (а спрятана карта 0). Леша говорит: «У меня либо набор 4, 5, 6, либо 1, 2, 0».

2. У Леши другой набор, скажем, 4, 5, 0 (а спрятана карта 6). Леша говорит: «У меня либо набор 4, 5, 0, либо 1, 2, 3».

В обоих случаях названный Лешей «не свой» набор пересекается с Гришиным как минимум по двум картам, поэтому Гриша тоже узнает, какой на самом деле набор у Леши. Докажем, что Коле ничего не ясно. Действительно, и в том, и в другом случае названо три набора карт: А, В и С. Наборы В и С пересекаются по двум картам, Гриша сказал: «У меня либо А, либо В», Леша сказал: «У меня либо А , либо С». Это означает, что либо у Гриши набор А, а у Леши – С, либо у Гриши – В, а у Леши – А. Поэтому три карты из набора А и две карты из пересечения наборов В и С могут оказаться как у Гриши, так и у Леши (в нашем примере это карты 1, 2, 3, 4 и 5). А из остальных двух карт наборов В и С (в нашем примере 6 и 0) одна закрытая, другая – у одного из игроков. Поэтому местоположение никакой из карт Коля вычислить не может.

2) Заметим, что предыдущий способ не работает: зная закрытую карту, Коля может всё определить.

Пусть Гриша занумерует карты числами от 0 до 6 (и объявит об этом вслух). Затем пусть Гриша и Леша по очереди назовут остатки от деления суммы номеров своих карт на 7. Тогда они узнают расклад: ведь остаток суммы Гриши плюс остаток суммы Леши плюс номер спрятанной карты должны давать 0 + 1 + 2 + 3 + 4 + 5 + 6 = 0 (mod 7). Так, например, если у Леши карты 1, 3, 4, а Гриша назвал остаток 4, то спрятана карта —4 – (1 + 3 + 4) = 2 (mod 7), значит, у Гриши карты 0, 5, 6.

Проверим, что Коля ничего не узнал. Его информация исчерпывается Гришиной суммой g и Колиной картой к (а Лешину сумму теперь Коля и сам может вычислить). Рассмотрим любую другую карту, пусть ее номер х. Покажем, что она входит в какой-нибудь набор из трех карт с суммой g , не содержащий к. Для этого дополним х парой карт с суммой номеров g – х. Таких пар ровно три при любом значении g – х (доказательство см. ниже). Из них две, возможно, не подходят из-за того, что туда входит карта с номером s или к , но как минимум одна пара остается. С ее помощью мы и создадим набор для Гриши (а набор для Леши получится автоматически). Например, если х = 3, то в нашем случае при g = 4 надо найти пару с суммой 4–3 = 1. Таких пар три: 1 = 0 + 1 = 2 + 6 = 3 + 5 (mod 7). Из них подходит только (0, 1}, то есть у Гриши мог быть набор 0, 1, 3.

Итак, любая карта могла оказаться у Гриши. Такие же рассуждения показывают, что любая карта могла оказаться и у Леши. Поэтому местоположение никакой из карт Коля вычислить не может.

Осталось доказать, что неупорядоченных пар с нужной суммой s всегда три. Есть семь упорядоченных пар (0, s), (1, s — 1)…, (6, s — 6). Из них ровно в одной оба остатка одинаковы, поскольку уравнение 2 х = s имеет, ввиду взаимной простоты чисел 2 и 7, ровно одно решение. Из неупорядоченной пары с разными остатками получается ровно две упорядоченных, поэтому неупорядоченных пар вдвое меньше, чем упорядоченных, то есть ровно 3.

Ответ.Могут в обоих случаях.

Д45. Из Петиных слов следует, что он не комиссар. Возможны два случая:

1) Петя – мафиози. Тогда он лжет и на самом деле знает, кто Дима, поэтому Дима – второй мафиози.

2) Петя – мирный житель.

Информации, которую Дима мог бы извлечь из Петиного высказывания, недостаточно, чтобы догадаться, кто комиссар. Поэтому если Дима говорит правду, то он сам и есть комиссар. А если лжет, то он – мафиози.