Инесса Раскина - Логика для всех. От пиратов до мудрецов

3), 4) Для получения отрицания достаточно заменить «можно» на «нельзя» или «невозможно». В пункте 3 верно утверждение. Например, можно сторону 20 разделить на 4 равных части, а сторону 15 – на 5 равных частей и провести через точки деления прямые, параллельные сторонам. В пункте 4 верно отрицание: площадь исходного квадрата нечетна, а предполагаемых частей – четна.

5) Пусть в школе n учеников. Каждый может иметь от 0 до n – 1 друга – всего n вариантов. Но все эти варианты одновременно реализоваться не могут: если у кого-то n – 1 друг (т. е. он дружит со всеми остальными учениками), то никто другой не может вообще не иметь друзей. Поэтому вариантов меньше, чем учеников, и какой-то вариант соответствует хотя бы двум ученикам.

6) Для формулировки отрицания убрать «не» недостаточно. Если уточнить: «Через любое отверстие…», то ясно, что это общее высказывание, к которому отрицание строится так: «В листке из школьной тетради можно прорезать такое отверстие, через которое может пролезть человек». С такими высказываниями мы еще встретимся на втором занятии. Как ни странно, верно именно отрицание. На рис. 21 показано, как вырезать подходящее отверстие. Чем чаще разрезы, тем более длинная и узкая «змейка» будет его ограничивать.

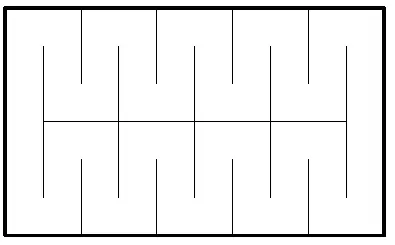
Рис. 21

2.9.1) Да, могут. Если все грибы съедобны. 2) Да, могут. Если в корзине есть и съедобные, и несъедобные грибы. 3) Да, могут. Если съедобных грибов вообще нет.

2.10.Нет, не является. Эти высказывания вполне могут выполняться одновременно.

2.11.Иллюстрации изображены на рисунке 22. Одинаковый смысл имеют третье и четвертое высказывания.

2.12.Денис не прав. Он путает высказывания «У всех великих людей плохой почерк» и «Все люди с плохим почерком– великие» (см. рис. 23).

2.13.Правду сказали все трое.

Комментарий.«Хотя бы один» означает «Ровно один или больше одного». В данном случае у Зайца «хотя бы один» означает «ровно один», у Волка – «двое», у Лисы – «все трое».

2.14.«Некоторые врачи имеют недостаточный опыт. Каждый врач хоть когда-нибудь ставил неправильный диагноз. Некоторые врачи опаздывают на работу. Некоторые пациенты недовольны лечением. Некоторые пациенты жалуются на бытовые условия. Никто не выздоравливает за один день».

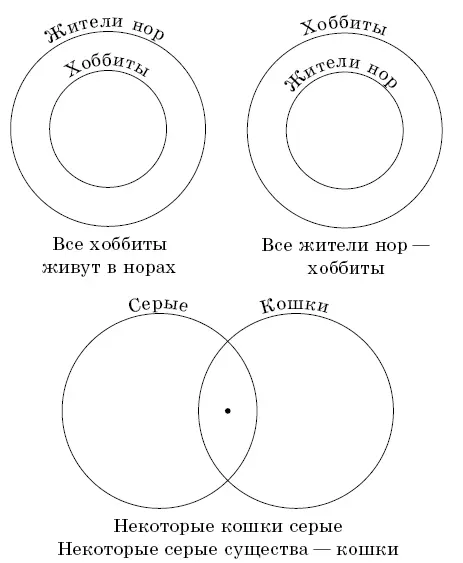
Рис. 22

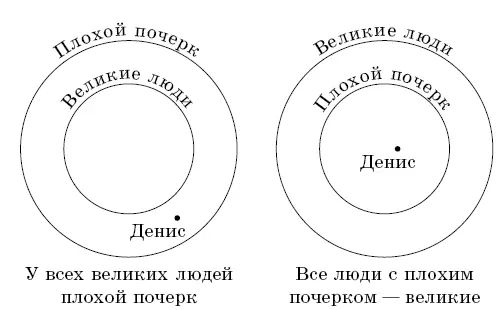
Рис. 23

2.15.Рыцарь не может сказать «Все мы лжецы», поэтому первый – лжец. Второй сказал правду: «Не все мы лжецы», поэтому он – рыцарь. В комнате больше трех человек (так как первый солгал), но не больше четырех (так как второй сказал правду), то есть ровно четыре. Поэтому третий солгал, и лжецов среди них меньше трех. А двух лжецов мы уже знаем – это первый и третий.

Ответ.Всего в комнате четверо. Лжецов из них двое: первый и третий.

2.16.Заведем на каждого человека досье:

Если у человека есть телевизор, будем писать Т, если нет— T.

Если человек является маляром, будем писать М, если нет— М.

Если человек каждый день купается в бассейне, будем писать Б, если нет— Б.

Например, про человека, не являющегося маляром, имеющего телевизор и каждый день купающегося в бассейне, напишем Т МБ. По этим трем признакам все люди делятся на 8 групп:

1) ТМБ; 2) ТМ Б; 3) Т МБ; 4) Т МБ;

5) TМБ; 6) TМ Б; 7) TМБ; 8) TМБ.

Условие «Среди людей, имеющих телевизоры, не все являются малярами» означает, что хотя бы в одной из двух групп, третьей и четвертой, есть хотя бы один человек. Условие «Люди, каждый день купающиеся в бассейне, но не являющиеся малярами, не имеют телевизоров» означает, что третья группа людей пуста. Значит, в четвертой группе кто-то есть. И эти люди (или человек) владеют телевизорами, но не каждый день купаются в бассейне.

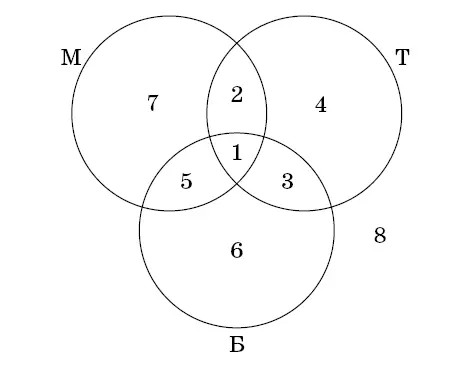
Рис. 24

Этому решению можно придать более наглядный вид (рис. 24). Вместо таинственных трехбуквенных кодов нарисуем три круга. В один поместим всех владельцев телевизоров, в другой – маляров, в третий – ежедневно посещающих бассейн. Людей, удовлетворяющих всем трем условиям, попросим разместиться на пересечении всех трех кругов, помеченном цифрой 1. Такие люди относятся к первой группе ТМБ. Люди из других групп тоже окажутся на территориях с прежними номерами. Восьмой группе предоставим территорию за пределами всех трех кругов. Дальнейшие рассуждения ничем не отличаются от предыдущей версии.