Феофан Бублейников - О движении

Пусть по концам невесомого рычага подвешены грузы Р и Q , уравновешивающие друг друга.

Архимед делает предположение, что груз Р разделен на 2m , а груз Q на 2n равных между собой частей. Эти грузики распределяются равномерно вдоль невесомого стержня длиной 2 (m + n) .

Если этот стержень подперт посередине, то грузики взаимно уравновесятся, потому что по каждую сторону от точки опоры будет одинаковое число грузиков, равное m + n.

Не нарушая равновесия, можно заменить действие 2m грузиков одним грузом Р , подвешенным посередине занятого ими расстояния.

Точно так же действие других 2n грузиков можно заменить грузом Q , подвешенным посередине расстояния, занятого этими грузиками.

Легко видеть, что точка подвеса груза Р находится от точки опоры рычага на расстоянии (m + n) — m = n , а точка подвеса Q на расстоянии (m + n) — n = m от нее.

Грузы Р и Q относятся друг к другу как P: Q = 2m: 2n = m: n , то-есть их равновесие сохраняется, если расстояния точек подвеса обратно пропорциональны весам грузов.

Вывод закона двуплечего рычага был началом учения о равновесии твердых тел — статики. Пользуясь этим законом, можно вывести условия равновесия блока, ворота, зубчатого колеса и других простых машин.

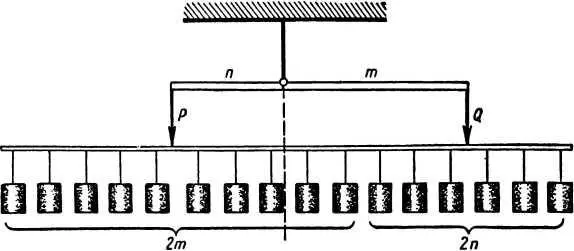
Вывод закона рычага, сделанный Архимедом.

Архимед не ограничился изучением равновесия твердых тел. Он заложил и основы гидростатики. На эти исследования его навело решение одного практического вопроса.

Правитель Сиракуз, царь Гиерон, заказал мастеру отлить из золота корону. Когда заказ был выполнен, возникло подозрение, что мастер утаил часть данного ему драгоценного металла. Однако корона весила столько же, сколько было выдано золота.

Как же узнать, не заменена ли часть золота серебром?

Решение этой задачи царь возложил на Архимеда.

Труднейшие проблемы Архимед решал всегда гениально просто. Так было и в этом случае.

Чем плотнее тело, тем меньше его объем при равном весе. А об объеме легко судить по количеству вытесняемой воды при погружении в нее тела.

Значит, если в короне содержится серебро, то ее объем будет больше объема того куска золота, который был выдан мастеру. С другой стороны, он будет меньше объема куска серебра, по весу одинакового с короной.

Архимед приказал дать ему кусок золота и кусок серебра такого же веса, как корона. После этого он погрузил в сосуд с водой золото, серебро и корону, собирая отдельно воду, вытесненную каждым из этих предметов.

Оказалось, что меньше всего воды вытеснил кусок золота, больше — корона и еще больше — кусок серебра. Так Архимед доказал, что корона отлита из сплава серебра и золота.

Архимед не ограничился решением заданной ему практической задачи. Из этого опыта он вывел общий закон: «тела, которые тяжелее жидкости, будучи опущены в жидкость, погружаются все глубже, пока не достигают дна, и, пребывая в жидкости, теряют в своем весе столько, сколько весит жидкость, взятая в объеме этих тел».

Этот закон было легко проверить, подвешивая тело под чашкой весов и опуская его в воду: весы показывали, что тело становилось как бы легче на вес вытесненной воды. Это, конечно, объясняется давлением снизу вверх, оказываемым водой на погруженное в нее тело, а не действительной «потерей веса».

В наше время закон Архимеда формулируется так: жидкость действует на погруженное в нее тело с силой, направленной вертикально вверх и равной весу жидкости в объеме погруженной в нее части тела.

Продолжая исследование равновесия жидкости и плавающих тел, Архимед исходил из единственного допущения, что «при равномерном и непрерывном расположении ее частиц менее сдавленная частица вытесняется более сдавленной» и «отдельные частицы этой жидкости испытывают давление отвесно расположенной над ними жидкости».

Архимед исследовал все случаи равновесия плавающих тел. Он указал, что тело, более легкое, чем жидкость, погружается ровно настолько, что вытесненная им вода по весу равна ему. Он вывел условия равновесия плавающего шарового сегмента и сегмента параболоида вращения (тела, образованного вращением параболы около ее оси).

Наконец, Архимед первый доказал, что «поверхность всякой жидкости, пребывающей в покое, имеет форму сферы, центр которой совпадает с центром Земли».