Михаил Гершензон - Головоломки профессора Головоломки. Сборник загадок, фокусов и занимательных задач

А «кировцы» три посадили у вас, а у себя сколько? Двадцать без шести – четырнадцать. Четырнадцать да три – это будет семнадцать, стало быть, на шесть меньше. Так они ведь и сами, гляди, против вас какие маленькие! Как комар против мухи.

– А у нас ведь в ряду не двадцать, – говорит Костя, – у нас в ряду восемьдесят деревьев.

– Ну и что? – сказал милиционер. – Сколько б у вас ни было в ряду деревьев, все равно, если станешь считать, получится то же самое.

Семенову не понравился этот ответ. Он пустил в ход свою любимую алгебру.

– Обозначим число деревьев в каждом ряду буквой n.

«Чапаевцы» посадили в своем ряду n – 3 и в чужом ряду 6 деревьев.

«Кировцы» посадили в своем ряду n – 6 и в чужом ряду 3 дерева.

Значит, чапаевцы всего посадили: n – 3 + 6 = n + 3.

А кировцы всего посадили: n – 6 + + 3 = n – 3.

Теперь ясно, что, сколько там ни было деревьев в ряду, «чапаевцы» на шесть деревьев больше «кировцев» посадили.

Семенов увидел на столе катушку, взял нитку, которая шла к нему из-под катушки, и потянул. Катушка покатилась не вперед, а назад

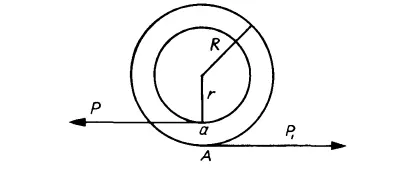
– Трубка катушки, – сказал Семенов, – имеет радиус r, колесо катушки – радиус R. К катушке приложены две силы: сила Р, с которой я тяну горизонтально за нитку влево, и сила противодействия Р 1, возникающая вследствие трения в точке А. Силы эти равные и противоположные. Сила Р стремится вращать катушку по часовой стрелке, сила Р 1– против часовой стрелки. Но сила Р приложена к малому радиусу r, сила Р 1– к большому радиусу R. Поэтому действие силы Р 1будет больше, чем действие силы Р, и катушка начнет вращаться против часовой стрелки. Точно так же можно объяснить и ваш фокус с велосипедом.

Допустим, что № 2 – Балхаш. Значит, № 3 – не Ладожское и № 4 – не Иссык-Куль. Если № 4 не Иссык-Куль, значит, № 1 – Ладожское. Если № 1 – Ладожское, значит, № 1 – не Байкал, а раз так, выходит, что Онежское – № 2, а это невозможно, потому что мы предположили, что № 2 – это Балхаш. Мы зашли в тупик. Значит, наше первое предположение неправильно: № 2 – это не Балхаш.

Тогда правильно, что № 3 – Ладожское и что № 4 – Иссык-Куль. Значит, Онежское не может быть № 3, зато правильно, что Байкал № 5, значит. Онежское – № 2, а Балхаш – № 1 Таким образом:

№ 1 – Балхаш,

№ 2 – Онежское,

№ 3 – Ладожское,

№ 4 – Иссык-Куль,

№ 5 – Байкал

Миля на ровном месте отнимала у путешественников 1/4 часа. Миля подъема – 1/3 часа, миля спуска – 1/6 часа. Значит, чтобы пройти любую милю дважды – на пути вперед и на пути назад, они тратили 1/2 часа, независимо от того, была ли это гора или ровное место. Таким образом, за 6 часов они прошли 12 миль вперед и 12 миль назад.

Если бы 12 миль пути вперед они шли почти сплошь по равнине, им потребовалось бы немногим больше 3 часов, если бы это был почти сплошной подъем, те же 12 миль отняли бы у них немногим меньше 4 часов. Поэтому с точностью до получаса можно определить время, потребовавшееся им на восхождение: 3 1/2 часа. А так как из дому путешественники вышли в 3 часа, то вершины они достигли в 6 1/2 (с точностью до получаса).

Валя Журавлева дала правильный ответ. Действительно, я ошибся, когда составлял эту задачу. Меня ввело в заблуждение название «морской единорог», и я не подумал, что у нарвала вовсе не рог, а зуб.

Все дело в том, что Семенов неправильно понял слово «вытесняет». Смысл закона Архимеда такой: когда какое-нибудь тело плавает в воде, часть этого тела погружена в воду; в воде при этом образуется как бы ямка. Представьте себе, что нам удалось бы вынуть плавающее тело из воды так, чтобы эта ямка осталась; теперь мы наливаем в нашу ямку воду из другого сосуда, пока не заполним ее. Нам придется налить для этого количество воды, равное по весу плававшему телу.

Поэтому совершенно не важно, было у вас в большом ведре много воды или мало, выплеснулась она на пол, когда вы погрузили в нее маленькое ведерко, или нет. Можно сказать совершенно точно: когда вы погрузили ведерко, вода между стенками ведер поднялась до какого-то уровня, и в ней образовалась определенной величины ямка.

Вес воды, которой можно было бы заполнить эту ямку, равняется весу всего вашего маленького, нагруженного шариками ведра. Вот что говорит закон Архимеда.