Лев Генденштейн - Алиса в стране математики

Алиса честно пыталась выполнить своё обещание — не думать о последнем моменте перед шестью часами. Но удивительное дело — чем больше она старалась об этом не думать, тем настойчивее это лезло ей в голову!

— Какой же момент, действительно, последний ? — крутилось у Алисы в голове помимо её воли. — Ведь даже когда до шести часов остаётся всего одна миллионная доля секунды, её снова можно разделить пополам — значит, есть и такой момент, когда до шести часов остаётся одна двухмиллионная доля секунды... но и этот момент не последний: делить пополам можно без конца... Делить без конца ! — воскликнула она про себя, и у неё вырвалось:

— Последнего момента нет вообще , потому что делить пополам можно без конца! Получается, что у этой загадки просто нет отгадки!

И тут Алиса увидела, что Заяц и Шляпник ужасно расстроились: Заяц готов был заплакать, а Шляпник утратил весь свой пыл и смотрел перед собой пустыми глазами.

— Но почему вас так огорчает, что последнего момента перед шестью часами нет? — удивилась Алиса.

— Неужели ты не понимаешь? — грустно сказал Шляпник. — Ведь если последнего момента нет, значит, шесть часов не наступят никогда ...

— Почему? — спросила Алиса.

— Потому что они могут наступить только после этого момента, а его-то как раз и нет ! — ответил Шляпник.

Тут Соня качнулся чуть сильнее и... свалился с чайника головой в торт!

Казалось бы, кому могут быть интересны загадки без отгадок, или, говоря языком математиков, задачи, у которых нет решений ? Однако именно такие задачи приковывали внимание математиков в течение тысячелетий: эти непокорные задачи были вызовом человеческому уму, и поэтому они интриговали математиков так же сильно, как сыщиков — тайны загадочных преступлений.

Вот история трёх знаменитых задач, пришедших из глубокой древности.

Первая задача называется «квадратура круга» : как построить круг и квадрат одинаковой площади, пользуясь только циркулем и линейкой без делений?

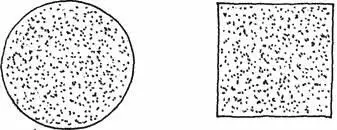
Примерно так выглядят круг и квадрат одинаковой площади — чтобы закрасить их одним и тем же слоем краски, понадобится одинаковое количество краски

Условие задачи кажется настолько простым, что за неё берётся даже тот, кто только начал знакомиться с геометрией, однако решить её не удалось даже величайшим математикам! Правда, Архимед придумал способ, как можно подойти к точному решению сколь угодно близко .

Шли века и тысячелетия, но задача о квадратуре круга оставалась непобедимой. И только в конце XIX века немецкий математик Линдеман нашёл неожиданное решение этой задачи: он строго доказал, что с помощью только циркуля и линейки построить круг и квадрат одинаковой площади невозможно ! Это доказательство произвело на математиков такое сильное впечатление, что Линдемана нарекли «победителем задачи о квадратуре круга». Такой титул говорит, что строгое доказательство отсутствия решения математики считают тоже решением : ведь решить задачу — это найти все решения или доказать, что решений нет !

Вторая знаменитая задача называется «удвоение куба» . О происхождении этой задачи существует даже легенда.

Однажды на острове Делос в Эгейском море вспыхнула эпидемия чумы. В те времена перед чумой были бессильны даже мудрые греки. Единственное, что они могли сделать — обратиться за помощью к богам. Однако беседовать с богами напрямую мог не каждый древний грек — этим занимались только «оракулы», то есть «предсказатели судеб». И вот оракул, посоветовавшись с богом искусств Аполлоном, объявил, что для спасения от чумы надо удвоить золотой жертвенник Аполлону. Этот жертвенник имел форму куба, и жители Делоса поспешили как можно скорей отлить из золота ещё один такой же куб и поставили его поверх первого.

Однако чума не прекратилась.

— Надо удвоить жертвенник, сохранив его форму , — объяснил оракул. — Новый жертвенник должен быть тоже кубом , но чтобы найти размеры нового куба, Аполлон разрешает вам пользоваться только циркулем и линейкой!

Бедные делосцы, не сумев сами решить эту задачу, обратились к знаменитому философу Платону (он так уважал математику, что над входом в сад, где он, прогуливаясь, занимался со своими учениками, велел начертать: «Пусть не входит сюда не знающий геометрии»). Однако и Платон не смог решить задачу об удвоении куба.