Татьяна Пушкарёва - Математические основы живописи и архитектуры

Кроме правильных и полуправильных многогранников красивые формы имеют звездчатые многогранники. Правильные звездчатые многогранники получаются из правильных многогранников путем продолжения их граней и ребер. Их всего четыре, и называются они телами Кеплера – Пуансо (рис. 4).

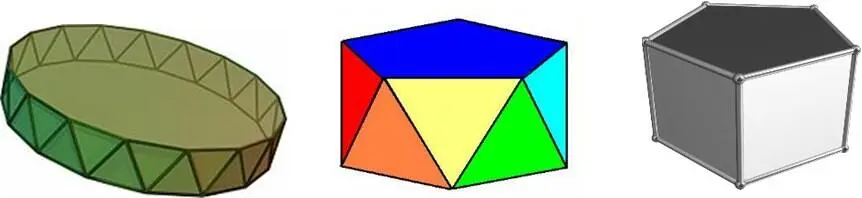
Рис. 3. Антипризмы

Рис. 4. Тела Кеплера–Пуансо

Тесселяции , известные также как покрытие плоскости плитками (tiling), являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов. Правильные тесселяции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодных для использования в правильных тесселяциях. Это правильный треугольник, квадрат и правильный шестиугольник (рис. 5).

Рис. 5. Правильные тесселяции

Полуправильными тесселяциями называют такие тесселяции, в которых использованы правильные многоугольники двух или трех типов и все вершины одинаковы (рис. 6).

Рис. 6. Полуправильные тесселяции

Существует всего 8 полуправильных тесселяций. Вместе три правильных тесселяции и восемь полуправильных носят название Архимедовых.

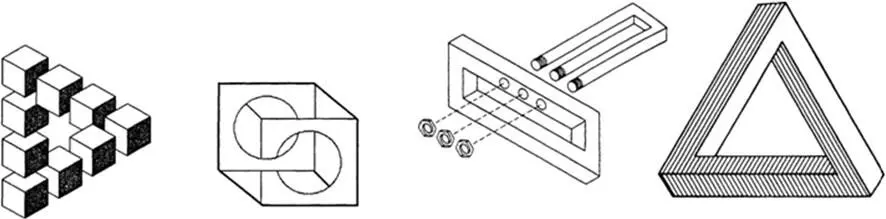
Рис. 7. Невозможные фигуры

Рис. 8. Ленты Мебиуса

Невозможные фигуры – это фигуры, изображенные в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве (рис. 7).

Лента Мебиуса – это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, если перекрутить один из концов полоски, а затем склеить оба конца друг с другом (рис. 8).

Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников. К ним также относится родственная область – анаморфное искусство . Слово анаморфный (anamorthic) состоит из двух греческих слов «ana» (снова) и «morthe» (форма). К анаморфным относятся изображения, настолько сильно искаженные, что разобрать их без специального зеркала бывает невозможно. Если смотреть в анаморфоскоп, то изображение «формируется снова» в узнаваемую картину.

Рис. 9. Фракталы

Фрактал – это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления так, что получается объект высокой сложности с множеством мелких деталей (рис. 9).

1. Какие фигуры и объекты наиболее часто используются в математическом изобразительном искусстве?

2. Что такое многогранник?

3. Какие многогранники относятся к Платоновым телам?

4. Что такое тело Архимеда?

5. Какие многогранники называют призмами и антипризмами?

6. Какие многогранники называют телами Кеплера – Пуансо?

7. Что такое тесселяции?

8. Какие тесселяции называют правильными и полуправильными?

9. Какая фигура называется невозможной?

10. Что представляет собой лента Мебиуса?

11. Какие изображения называют анаморфными?

12. Что такое фрактал?

Аксонометрия – метод проектирования взаимно параллельными лучами, наклонными к плоскости проекций. Термин аксонометрия представляет сочетание двух греческих слов – «ось» и «мерить». Название точно определяет процесс построения аксонометрических изображений, основанный на воспроизведении размеров проектируемого предмета по направлениям трех осей – длины, ширины и высоты.

К изображениям в аксонометрических проекциях в работах архитекторов, инженеров и художников предъявлялись различные требования, поэтому были созданы особые виды таких проекций для различных целей.