Георгий Димитриади - Введение в финансовую математику

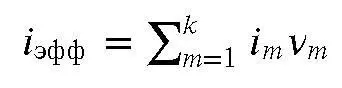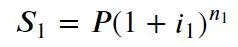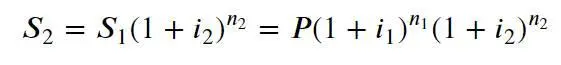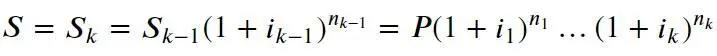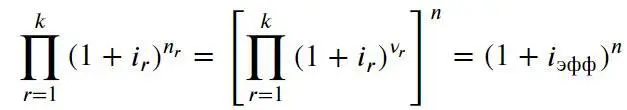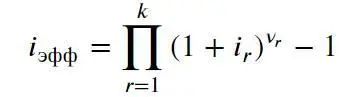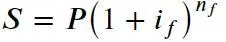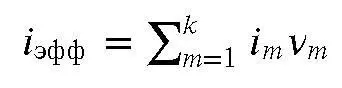
рассчитываемой как взвешенная сумма процентных ставок каждого периода. Эту ставку можно использовать как единый эквивалент для расчета наращенной суммы:

S = P (1 + i эфф n ).

Теперь перейдем к аналогичному расчету с использованием методики сложных процентов. По истечении первого периода n 1наращенная сумма составит:

.

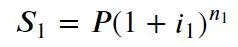
Поскольку сложные проценты начисляются на капитализированную сумму, после второго периода n 2наращенная сумма составит:

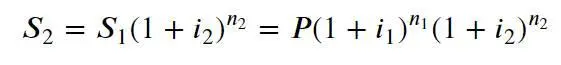
После k -ого периода n k найдем требуемую наращенную сумму:

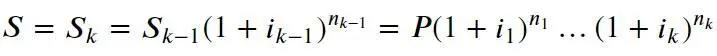
Из полученной формулы можно сделать следующие выводы, аналогичные тем, что были сделаны ранее для простых процентов: размер наращенной суммы не зависит от порядка чередования периодов с различными процентными ставками. Кроме того, если в два или более периода имело место одна и та же процентная ставка, то для целей расчета наращенной суммы их можно объединить в один, длительность которого равна сумме длительностей исходных промежутков.

Аналогично предыдущему можно ввести понятие эффективной ставки сложных процентов (см. подробнее об этом ниже):

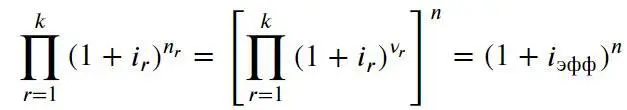
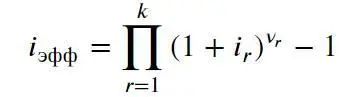
Здесь ν r = n r / n – доля промежутка n r в полном сроке рассматриваемого кредита. Получается, что для случая с переменной процентной ставкой можно ввести понятие эффективной процентной ставки сложных процентов, рассчитываемой как взвешенное произведение процентных ставок каждого периода, и которую можно использовать как единый эквивалент для расчета наращенной суммы:

S = P (1 + i эфф ) n .

Сложные проценты с начислением чаще, чем раз в год

Во всех рассуждениях ранее при использовании сложных процентов предполагалось, что они начисляются один раз в год. Однако на практике встречаются случаи, когда начисление происходит чаще. Пусть оно происходит m раз в год, где m – натуральное число. Например, начисление может происходить ежемесячно ( m = 12).

Для сложных процентов с начислением один раз в год была получена формула:

S = P (1 + i ) n .

Теперь мысленно предположим, что в рассуждениях, из которых была выведена эта формула, период времени «год» будет заменен на период времени «1/ m года» или « m -ая доля года». Поскольку все рассуждения останутся в силе, получим формулу:

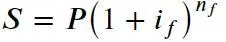
где i f – процентная ставка за « m -ую часть года», n f – срок, отраженный в «m-ых частях года» (а не в годах, как ранее). Для того, чтобы вернуться к используемым ранее обозначениям выразим i f и n f через годовые переменные:

i f = i / m , n f = mn .

Последнее соотношение легко интерпретируемо: при сроке n лет количество периодов размером «1/ m года» равно mn .

Тогда с использованием годовой процентной ставки итоговую формулу расчета наращенной суммы с использованием сложных процентов с начислением m раз в год можно записать как:

S = P (1 + i / m ) mn .

Поскольку, как было выяснено, формула сложных процентов с начислением m раз в год верна и для нецелого числа лет n , то и полученная формула верна для нецелого n . Более того, можно показать, что она остается верной и для нецелого m .

Отметим, что всегда предполагается, что сложные проценты начисляются один раз в год, если не указано противное.

Дня того, чтобы продемонстрировать зависимость наращенной суммы от количества начислений m раз в год, сведем в Таблицы 2 и 3 результаты расчетов при Р = 100 руб. и ставке i = 10% в Таблице 2 и ставке i = 25% в Таблице 3.

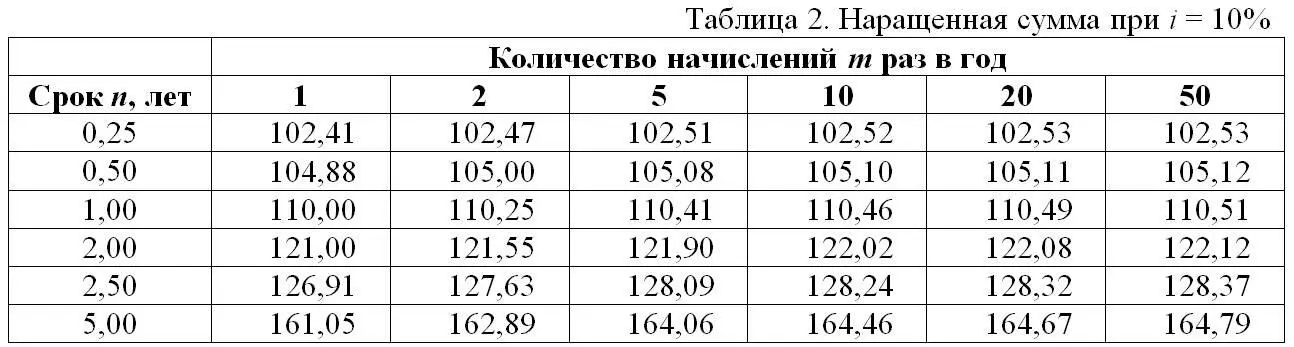
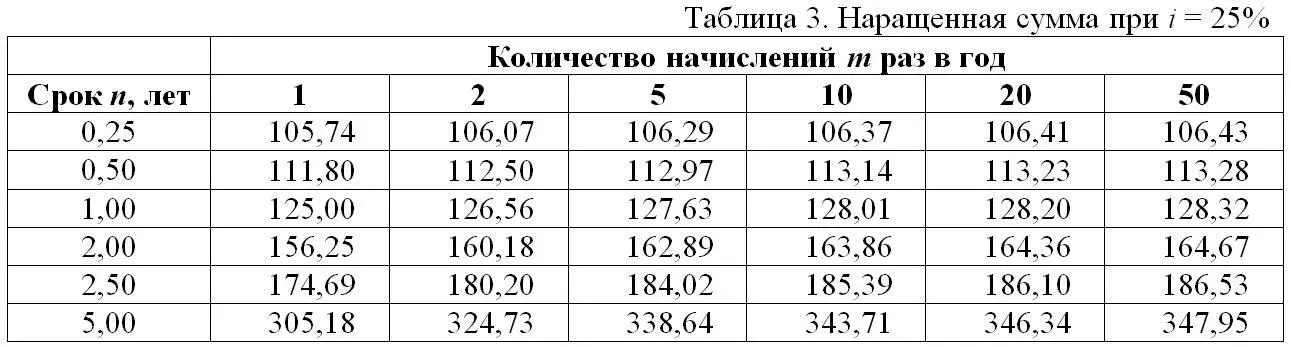
Дискретное и непрерывное начисление процентов