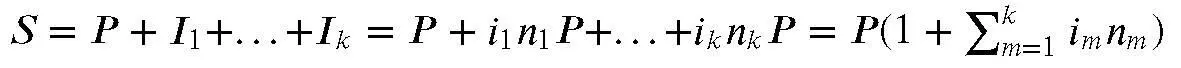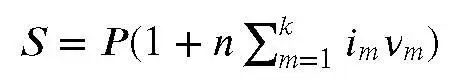Георгий Димитриади - Введение в финансовую математику

Нецелые значения срока

В формулах наращения простых и сложных процентов срок n может быть как целым числом (целое число лет), так и нецелым.

Действительно, для простых процентов процентных доход прямо пропорционален сроку. Соответственно, срок может быть любым: год, полтора, любая доля года и др.

Для сложных процентов нецелое число лет является логичным обобщением концепции капитализации. Например, срок в 2,5 года означает два полных года и еще половину, то есть два годовых начисления процентов и еще одно «половинное» начисление по истечении полугода.

Сравнение простых и сложных процентов

Предположим, что выдаются два кредита с одинаковой начальной суммой P и одинаковой процентной ставкой i на одинаковый срок n лет, но для первого кредита проценты начисляются по формуле простых процентов, а для второго – по формуле сложных процентов. Давайте сравним суммы начисленного процентного дохода.

Для простых процентов функция

S = P (1 + in )

представляет собой линейную функцию от n , а для сложных:

S = P (1 + i ) n –

показательную.

Сделаем иллюстративной расчет для случая P = 100 руб., различных сроков n и значений процентной ставки i . Полученные значения наращенной суммы S приведены в Таблице 1.

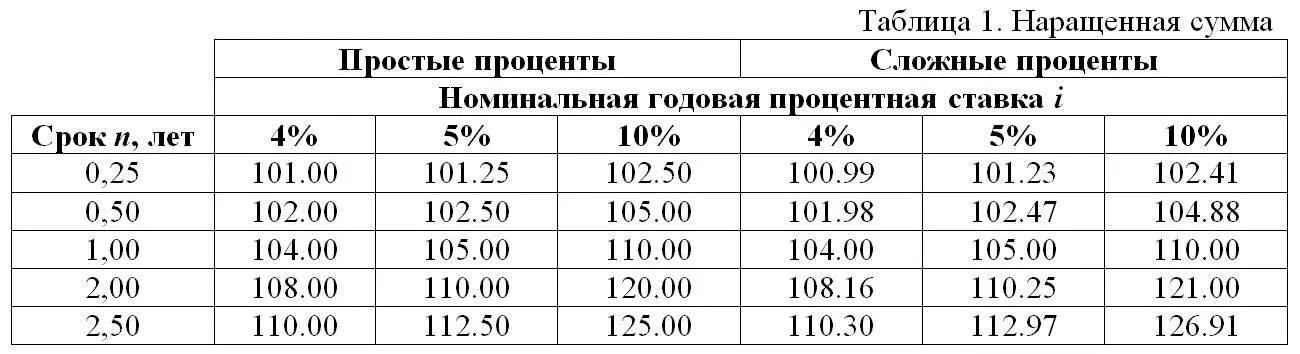
Изучив таблицу, легко увидеть, что при сроке меньше года наращенная сумма при расчете по формуле простых процентов превышает наращенную сумму при расчете по формуле сложных процентов, а при сроке более года – наоборот.

Для полного понимания изобразим на Рис. 1 график зависимости S ( n ) для сложных и простых процентов.

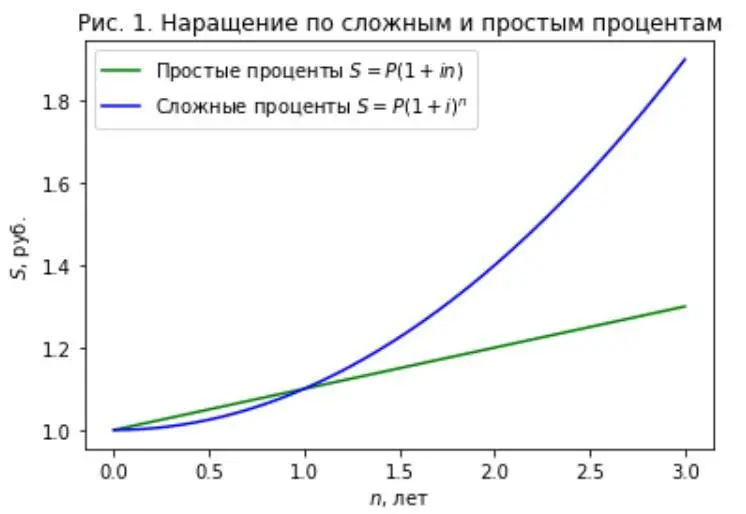
Из графика видно, что при сроке меньше года простые проценты превышают сложные, а при сроке более года – наоборот. Пользуясь этим, банки иногда в кредитных договорах устанавливают начисление процентов по формуле простых процентов при сроках до года и по формуле сложных процентов – в остальных случаях.

Различные процентные ставки

Процентная ставка рассматриваемого кредита может быть как фиксированной (постоянной), так и переменной, в зависимости от условий договора. Примером переменной ставки является ставка вида «LIBOR 1 1 Лондонская межбанковская ставка предложения ( англ. London Interbank Offered Rate, LIBOR) – средневзвешенная процентная ставка по межбанковским кредитам, предоставляемым банками, выступающими на лондонском межбанковском рынке с предложением средств в разных валютах и на разные сроки – от одного дня до 12 месяцев. Ставка фиксируется Британской Банковской Ассоциацией, начиная с 1985 года ежедневно в 11:00 по западноевропейскому времени на основании данных, предоставляемых избранными банками. + 1,5%». Ставки такого рода часто применяются на западных рынках. Произведем расчет наращенной суммы в случае переменной ставки.

Предположим, что ставка кредита меняется в течение его срока. Пусть полный срок кредита n разбит на периоды длины n 1, …, n k лет, причем в течение первого периода действовала процентная ставка i 1, в течение второго периода – i 2, …, в течение k -ого периода – i k .

Тогда в случае расчета по формуле простых процентов процентный доход за промежуток времени n 1будет:

I = in 1 P ,

…,

за промежуток времени n k :

I = in k P .

В итоге наращенная сумма составит:

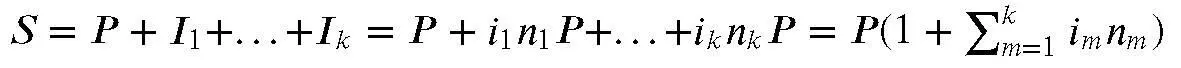
Из полученной формулы можно сделать следующие выводы. Размер наращенной суммы не зависит от порядка чередования периодов с различными процентными ставками. Кроме того, если в два или более периода имело место одна и та же процентная ставка, то для целей расчета наращенной суммы их можно объединить в один период, длительность которого равна сумме длительностей исходных.

Формулу можно переписать еще и так:

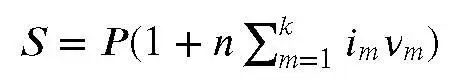
где ν m = n m / n – доля промежутка n m в полном сроке n рассматриваемого кредита. Получается, что для случая с переменной процентной ставкой можно ввести понятие эффективной процентной ставки простых процентов (см. об эффективных ставках подробнее ниже)