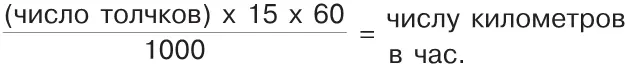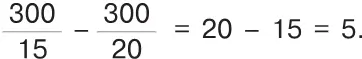Задача рассчитана на невнимательность читателя, который может подумать, что между 1 часом 20 минутами и 80 минутами есть разница. Как ни странно, но людей, попадающихся на этот крючок, оказывается немало, притом среди привыкших делать расчеты их больше, чем среди малоопытных вычислителей. Причина кроется в привычке к десятичной системе мер и денежных единиц. Видя обозначение «1 час 20 минут» и рядом с ним «80 минут», мы невольно оцениваем различие между ними, как разницу между 1 рублем 20 копейками и 80 копейками. На эту психологическую ошибку и рассчитана задача.
Головоломный вопрос решается очень просто. Передний паровоз тянет не весь состав, а только часть его, примерно половину вагонов. Остальные вагоны подталкиваются задним паровозом. У первой части состава сцепка вагонов натянута, у остальной она свободна, и вагоны упираются буфер в буфер.
Вы заметили, конечно, что при езде в вагоне ощущаются все время мерные толчки; никакие рессоры не могут сделать их неощутимыми. Толчки эти происходят оттого, что колеса слегка сотрясаются в местах соединения двух рельсов и толчок передается всему вагону.
Эти-то неприятные толчки, довольно разрушительно действующие на вагоны и рельсы, можно использовать для определения скорости поезда. Стоит лишь сосчитать, сколько толчков в минуту испытывает вагон, чтобы узнать, сколько рельсов пробежал поезд. Остается умножить это число на длину каждого рельса, — и вы получите расстояние, проходимое поездом в минуту.
Обычная длина рельса — около 15 м (выйдя на станции из вагона, вы можете, измеряя рельсы шагами, узнать их длину; каждые семь шагов можно принять за 5 м). Сосчитав с часами в руках число толчков в минуту, умножьте это число на 15, затем на 60 и делите на 1000 — получится число километров, пробегаемое поездом в час:
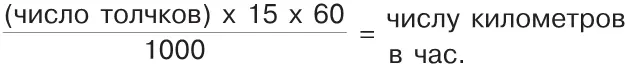
Более быстрый поезд прошел до точки встречи путь во столько же раз длиннее пути медленного поезда, во сколько раз скорость быстрого поезда превышает скорость медленного. После встречи быстрому поезду оставалось пройти до станции путь, пройденный до встречи медленным поездом, и наоборот.
Другими словами, быстрый поезд после встречи прошел путь во столько раз короче, во сколько раз больше его скорость. Если обозначить отношение скоростей через х, то на прохождение части пути от места встречи до станции быстрый поезд употребил в х 2меньше времени, чем медленный. Отсюда х 2= 2 1/4, и × = 1 1/2, то есть скорость одного поезда в полтора раза больше скорости другого.
Как поезд трогается с места?
Когда поезд, прибыв на станцию, останавливается, сцепка вагонов натянута. Если паровоз станет тянуть состав в таком виде, ему придется сдвигать с места весь состав сразу, при тяжелом составе это ему не под силу. Другое дело, когда паровоз предварительно подал состав назад; сцепка тогда не натянута, и приводится в движение вагон за вагоном последовательно, — это гораздо легче.
Короче говоря, машинист делает то же самое, что и возница тяжело нагруженного воза: он вскакивает на него только на ходу, когда движение уже началось; иначе лошади пришлось бы брать с места чересчур значительный груз.
1
4
1
2
Вторая лодка опоздала потому, что двигалась с 24-километровой скоростью меньшее время, чем с 16-километровой. Действительно, с 24-километровой скоростью она двигалась 24/24, то есть 1 час, а с 16-километровой — 24/26, то есть 1 1/2 часа. Поэтому она на пути туда потеряла времени больше, чем выгадала на обратном пути.
Плывя по течению, пароход делает 1 км в 3 минуты; плывя против течения — 1 км в 4 минуты. На каждом километре пароход в первом случае выгадывает 1 минуту, а так как на всем расстоянии он выгадывает 5 часов, или 300 минут, то, следовательно, от Энска до Иксограда 300 км.
Действительно:
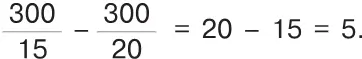
Конец ознакомительного отрывка
Купить книгу