Что касается веса такого кольца, то, если обыкновенное колечко весит, скажем, один золотник, такого же фасона кольцо из страны великанов должно было весить 1728 золотников, т. е. немногим менее полупуда.
Если исходить из размеров современной книги обычного формата (сантиметров 25 длиной и 12 шириной), то описанное Гулливером представится несколько преувеличенным. Чтобы читать книгу менее 3 метров вышины и полутора метров ширины, можно обойтись без лестницы и нет надобности ходить вправо и влево на 8–10 шагов. Но во времена Свифта, в начале XVIII века, обычный формат книг (фолиантов) был гораздо больше, чем теперь. Фолиант, например, «Арифметики» Магницкого, вышедшей при Петре Великом, — имел размеры: около 30 сантиметров в высоту и 20 в ширину. Увеличивая в 12 раз, получаем для книг великанов более внушительные размеры: 360 сантиметров (почти 4 метра) в высоту и 240 см в ширину (2 1/2 метра). Читать четырехметровую книгу без лестницы нельзя; но и тут не пришлось бы, переходя от одной строки к другой, делать 8–10 шагов, так что последняя подробность у Свифта безусловно является преувеличением.
Подобный фолиант должен весить в 1728 раз больше, нежели наш, т. е. пудов 70–80. Считая, что в нем 500 листов, получаем для каждого листа книги великанов вес около 11–13 фунтов. Перелистывать такие страницы, конечно, не трудно.

Буквы в книгах великанов имели около 2–3 см высоты; читать такую крупную печать с расстояния 10 футов, как читал Гулливер, очень удобно.
Окружность шеи великанов была больше окружности шеи нормального человека во столько же раз, во сколько раз был больше ее поперечник, т. е. в 12 раз. И если нормальному человеку нужен воротничок номер 40, то для великана понадобился бы номер 40 x x 12 = 480.
Мы видим, что у Свифта все, казалось бы, столь причудливые образы его фантазии тщательно рассчитаны. Пушкин в ответ на некоторые упреки критиков «Евгения Онегина» заметил, что в его романе «время расчислено по календарю». С таким же правом мог бы Свифт сказать о «Гулливере», что все его образцы добросовестно рассчитаны по правилам геометрии (но не правилам механики — в этом отношении можно сделать Свифту существенные упреки).
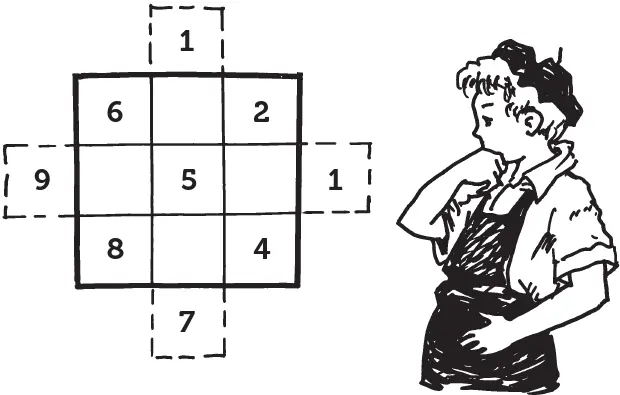
Наименьший магический квадрат
Составление магических, или волшебных, квадратов — старинный и еще сейчас весьма распространенный вид математических развлечений. Задача состоит в отыскании такого расположения последовательных чисел (начиная с 1) по клеткам разграфленного квадрата, чтобы суммы чисел во всех строках, столбцах и по обеим диагоналям квадрата были одинаковы.
Наименьший магический квадрат — 9-клеточный; легко убедиться испытанием, что магический квадрат из четырех клеток существовать не может. Вот образчик 9-клеточного магического квадрата:
Сложим ли мы в этом квадрате числа 4 + + 3 + 8, или 2 + 7 + 6, или 3 + 5 + 7, или 4 + + 5 + 6, или любой другой ряд из трех чисел, мы во всех случаях получим одну и ту же сумму 15. Итог этот можно предвидеть, не составляя еще самого квадрата: три строки квадрата — верхняя, средняя и нижняя — должны заключать все его 9 чисел, составляющие в сумме
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
С другой стороны, сумма эта должна быть равна, очевидно, утроенному итогу одной строки. Отсюда для каждой строки имеем итог:
45: 3 = 15.
Подобным же образом можно заранее определить сумму чисел строки или столбца любого другого математического квадрата, состоящего из какого угодно числа клеток. Для этого нужно сумму всех чисел квадрата разделить на число его строк.
Составив один магический квадрат, легко получить его видоизменения, то есть найти ряд новых магических квадратов. Если, например, мы составили квадрат (рисунок а ), то, повернув его мысленно на четверть полного оборота (на 90°), получим другой математический квадрат (рисунок б ):
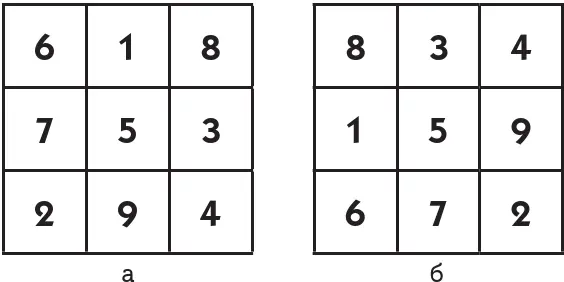
Дальнейшие повороты — на 180° (половину полного оборота) и на 270° (три четверти полного оборота) — дадут еще два видоизменения начального квадрата.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
















