Яков Перельман - Головоломки и развлечения

Каждый из вновь полученных магических квадратов можно, в свою очередь, видоизменить, если представить себе, что он как бы отражен в зеркале. На рисунке ниже показаны начальный квадрат и одно из его зеркальных отражений.

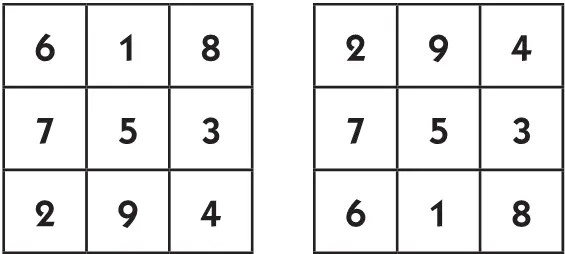
Проделав с 9-клеточным квадратом все повороты и отражения, получаем следующие его видоизменения:

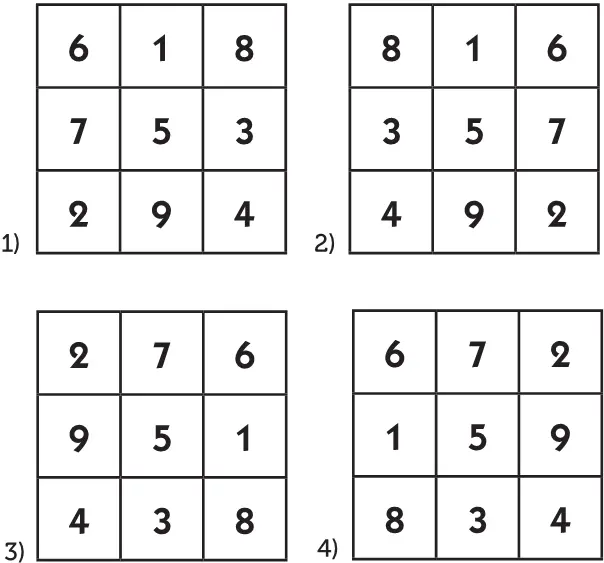
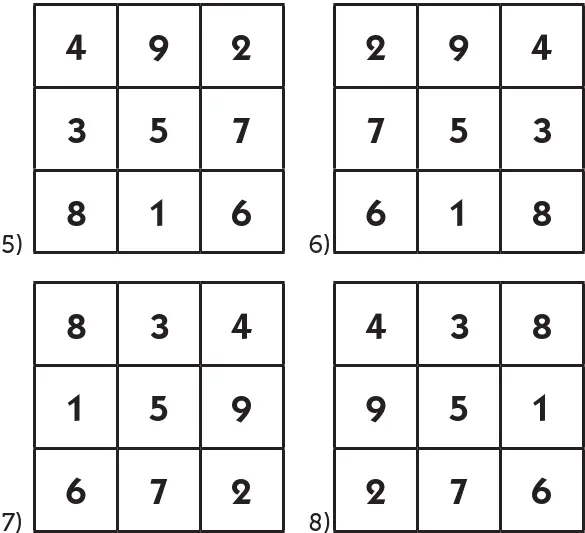
Это полный набор всех магических квадратов, какие вообще могут быть составлены из первых девяти цифр.

Познакомимся со старинным приемом составления нечетных магических квадратов, то есть квадратов из любого нечетного числа клеток: 3 × 3, 5 × 7, 7 × 7 и т. п. Прием этот предложен в XVII веке французским математиком Баше. Так как способ Баше пригоден, между прочим, и для 9-клеточного квадрата, то удобнее всего начать описание способа именно с этого наиболее простого примера. Итак, приступим к составлению 9-клеточного магического квадрата по способу Баше.

Начертив квадрат, разграфленный на девять клеток, пишем по порядку числа от 1 до 9, располагая их косыми рядами по три в ряд, как показано на рисунке.

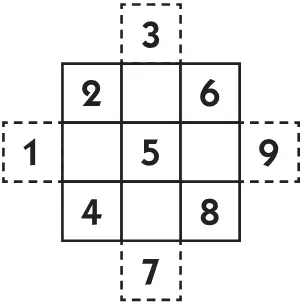
Числа, стоящие вне квадрата, вписываем внутрь его так, чтобы они примкнули к противолежащим сторонам квадрата (оставаясь в тех же столбцах или строках, что и раньше).

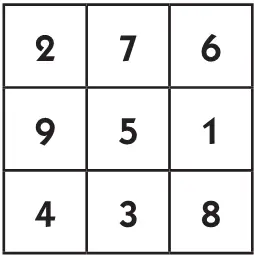
В результате получаем квадрат:

Применяем правило Баше к составлению квадрата из 5 × 5 клеток. Начинаем с расположения:

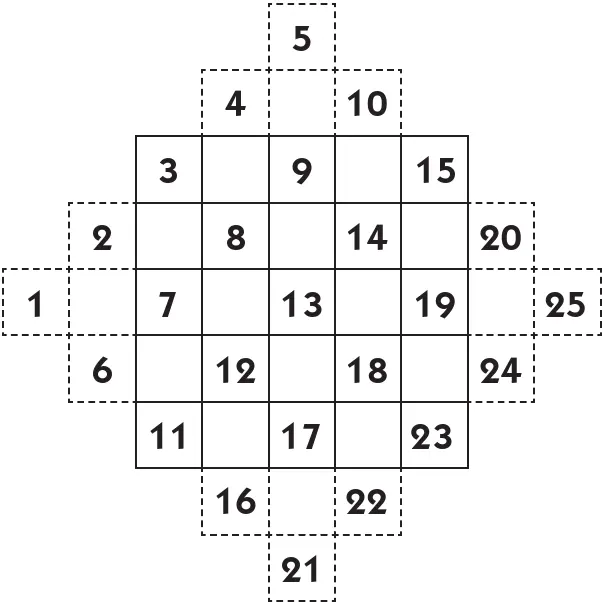
Остается только числа, оказавшиеся за рамками квадрата, ввести внутрь его. Для этого нужно фигуры, образованные числами, состоящими вне квадрата («террасы»), мысленно вдвинуть в квадрат так, чтобы эти фигуры примкнули к противолежащим сторонам квадрата. Получится магический 25-клеточный квадрат.

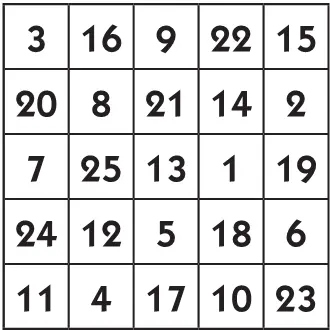
Обоснование этого простого приема довольно сложно; читатели могут удостовериться на практике, что способ правилен.

Составив один магический квадрат из 25 клеток, вы путем поворотов и отражений можете получить его видоизменения.

Способ Баше, или, как его иначе называют, «способ террас», — не единственный для составления квадратов с нечетным числом клеток. Из других существующих способов сравнительно несложен весьма древний прием, придуманный, как полагают, в Индии еще до начала нашего летоисчисления. Его можно изложить кратко в шести правилах. Внимательно прочтите все правила, а затем проследите их применение на примере магического квадрата из 49 клеток:

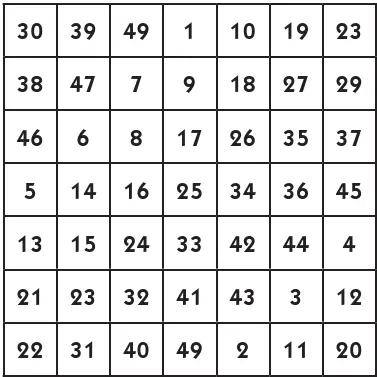
1. В середине верхней строки пишут 1, а в самом низу среднего справа столбца — 2.

2. Следующие числа пишут по порядку в диагональном направлении вправо и вверх.

3. Дойдя до правого края квадрата, переходят к крайней левой клетке ближайшей вышележащей строки.

4. Дойдя до верхнего края квадрата, переходят к самой нижней клетке соседнего справа столбца.

Примечание. Дойдя до правой верхней угловой клетки, переходят к левой нижней.

5. Дойдя до уже занятой клетки, переходят к клетке, лежащей непосредственно под последней заполненной клеткой.

6. Если последняя заполненная клетка находится в нижнем ряду квадрата, переходят к самой верхней клетке в том же столбце.

Руководствуясь этими правилами, можно быстро составлять магические квадраты с любым нечетным числом клеток.

Если число клеток квадрата не делится на 3, можно начинать составление магического квадрата не по правилу 1, а по другому правилу.

Единицу можно написать в любой клетке диагонального ряда, идущего от средней клетки крайнего левого столбца к средней клетке самой верхней строки квадрата. Все последующие числа вписываются согласно правилам 2–5.