Юлия Орлова - Основы управления предприятием

Язык SL позволяет строить разнообразные типы диаграмм и схем в IDEF5. Основная цель всех этих диаграмм – наглядно и визуально представлять основную онтологическую информацию.

Несмотря на кажущееся сходство, семантика и обозначения схематичного языка SL существенно отличается от семантики и обозначений других графических языков. Дело в том, что часть элементов графической схемы SL может быть изменен или вовсе не приниматься во внимание языком EL. Причина этого состоит в том, что основной целью применения SL является создание лишь вспомогательной структурированной конструкции онтологии, и графические элементы SL не несут достаточной информации для полного представления и анализа системы, тем самым они не предназначены для сохранения при конечном этапе проекта. Тщательный анализ, обеспечение полноты представления структуры данных, полученных в результате онтологического исследования, являются задачей применения языка EL.

Рис. 1.3.10. Схематические графические изображения IDEF5

Виды схем и диаграмм IDEF5

Как правило, наиболее важные и заметные зависимости между объектами всегда являются преобладающими, когда конкретные люди высказывают свои знания и мнения, касающиеся той или иной системы. Подобные взаимосвязи явным образом описываются языками IDEF5. Всего существует четыре основных вида схем, которые наглядно используются для накопления информации об онтологии в достаточно прозрачной графической форме.

1. Диаграмма классификации. Диаграмма классификации обеспечивает механизм для логической систематизации знаний, накопленных при изучении системы. Существует два типа таких диаграмм: Диаграмма строгой классификации (Description Subsumption – DS)и диаграмма естественной или видовой классификации (Natural Kind Classification – NKC). Основное отличие диаграммы DS заключается в том, что определяющие свойства классов высшего и всех последующих уровней являются необходимым и достаточным признаком принадлежности объекта к тому или иному классу. На рисунке 1.3.11 приведен пример такой диаграммы, построенной на основе тривиальной возможности классификации многоугольников по количеству углов. Из геометрии известно точное математическое определение многоугольника, суть определяющих свойств родительского класса. Определяющим свойством каждого дочернего класса дополнительно является количество углов в многоугольнике. Очевидно, зная это определяющее свойство для любого многоугольника, можно однозначно отнести его к тому или иному дочернему классу. С помощью диаграмм DS, как правило, классифицируются логические объекты.

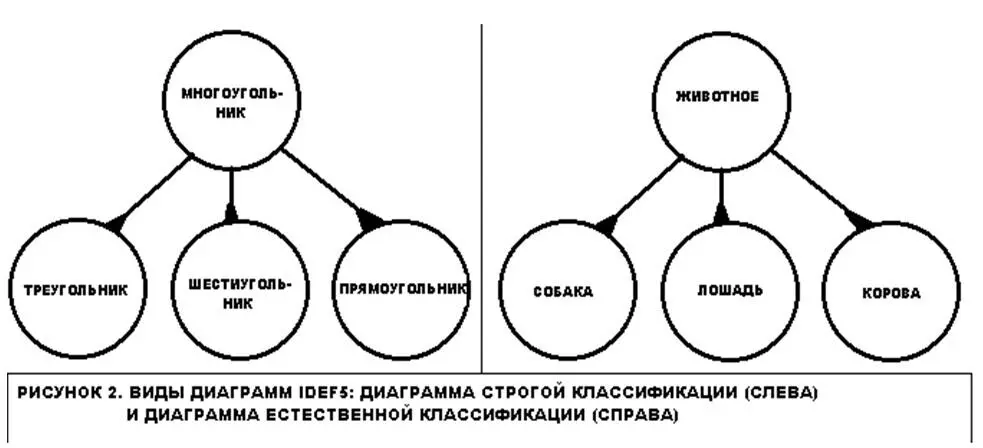
Рис. 1.3.11. Виды диаграмм IDEF5:диаграмма строгой классификации (слева) и диаграмма естественной классификации (справа)

2. Диаграммы естественной классификации или же диаграммы NKC, наоборот, не предполагают того, что свойства класса являются необходимым и достаточным признаком для принадлежности к ним тех или иных объектов. В этом виде диаграмм определение свойств класса является более общим. Пример такой диаграммы также приведен на рис. 1.3.12.

Композиционная схема. Композиционные схемы (Composition Schematics)являются механизмом графического представления состава классов онтологии и фактически представляют собой инструменты онтологического исследования по принципу "Что из чего состоит". В частности, композиционные схемы позволяют наглядно отображать состав объектов, относящихся к тому или иному классу. На рисунке 1.3.12 изображена композиционная схема шариковой ручки, относящейся к классу шариковых автоматических ручек. В данном случае шариковая ручка является системой, к которой мы применяем методы онтологического исследования.

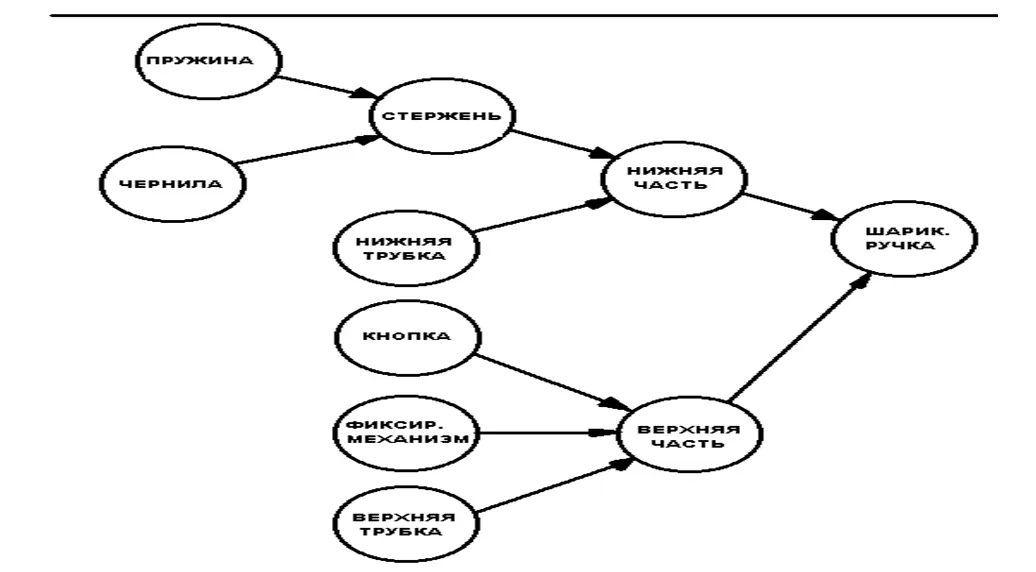
Рис. 1.3.12. Пример композиционной схемы

С помощью композиционной схемы мы наглядно документируем, что авторучка состоит из нижней и верхней трубки, нижняя трубка в свою очередь включает в себя кнопку и фиксирующий механизм, а верхняя трубка включает в себя стержень и пружину.

3. Схема взаимосвязей. Схемы взаимосвязей (Relation Schematics)позволяют разработчикам визуализировать и изучать взаимосвязи между различными классами объектов в системе. В некоторых случаях схемы взаимосвязей используются для отображения зависимостей между самими же классовыми взаимосвязями. Мотивацией для развития подобной возможности послужило то тривиальное правило, что все вновь разработанные концепции всегда базируются на уже существующих и изученных. Это тесно согласуется с теорией Новака и Гоуэна (Novak & Gowin, 1984), суть которой в том, что изучение любой системы часто происходит от частного к общему, то есть, происходит изыскание и исследование новой частной информации, влияющее на конечные характеристики более общей концепции, к которой эта информация имела прямое отношение. Исходя из этой гипотезы, естественным образом изучения новой или плохо понимаемой взаимосвязи является соотнесение ее с достаточно изученной взаимосвязью, для исследования характеристик их сосуществования.