Александр Краснов - Волчок и применение его свойств

Под воздействием удара волчок наклонится влево, точка А на диске станет при этом двигаться вниз, а точка В — вверх. Однако по закону инерции обе точки, стремясь сохранить прежнее направление движения, окажут сильное сопротивление действию удара. В результате этого возникает так называемая прецессионная сила, увлекающая волчок в сторону от направления действующей силы.

Внимательно наблюдая за проводимым опытом, мы заметим, что волчок, вращающийся против часовой стрелки, если смотреть сверху, отскакивает всегда под прямым углом влево от направления действующей на него силы (рис. 12).

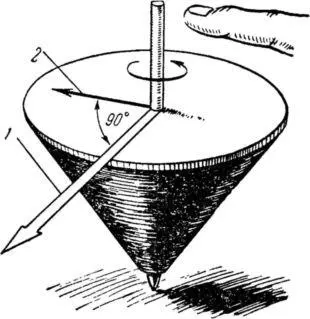
Рис. 12. Поведение быстро вращающегося волчка в случае толчка пальцем по его оси. 1 — направление силы процессии, уводящей волчок в сторону от валящей его силы; 2 — направление силы толчка.

Проделав подобный же опыт с волчком, вращающимся по часовой стрелке, обнаружим, что он отскакивает вправо от направления толчка также под прямым углом.

Проделав одну за другой несколько попыток свалить быстро вращающийся волчок, мы обнаружим, что при каждом толчке усиливается покачивание его оси. Наконец, оно окажется значительным. Теперь нетрудно заметить, что ось волчка описывает в пространстве определенную фигуру (рис. 13).

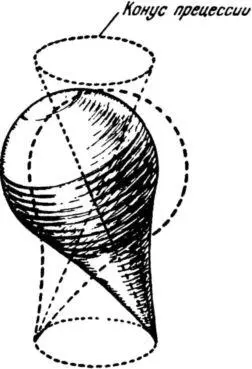
Рис. 13. Прецессия волчка.

Это так называемая прецессия волчка.

Стремление волчка устойчиво сохранять свое положение можно отчасти объяснить законом инерции. Но легкое покачивание оси объясняется и другим важным законом механики. Попытаемся разобраться в причинах этого явления на следующем простом примере.

Покатим с какой-нибудь постоянной скоростью по горизонтальной поверхности тяжелый металлический шар, оставляющий после себя след в виде черной черты (рис. 14, А ).

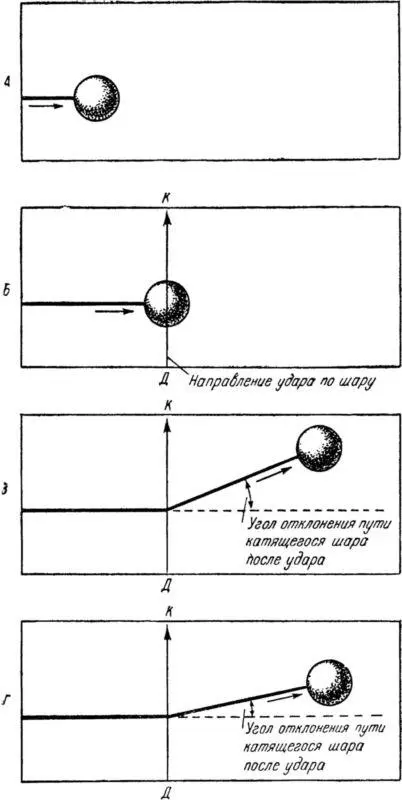
Рис. 14. Опыт с катящимся шаром .

Когда шар достигнет линии ДК , нанесем по нему быстрый удар под прямым углом к направлению движения (рис. 14, Б ).

В результате этого удара произойдет незначительное изменение первоначального направления, причем шар теперь покатится с несколько большей скоростью (рис. 14, В ).

Если сильно увеличить скорость движения шара и затем нанести по нему удар с прежней силой, то направление движения изменится еще меньше, чем в первом случае (рис. 14, Г ).

Проводя подобные опыты, мы в любом из них обнаружим, что всякая сила, приложенная к движущемуся телу, вызывает изменение его скорости. Это, безусловно, верно. Здесь действует второй закон Ньютона: всякая сила, приложенная к движущемуся телу вызывает изменение его скорости.

Движение быстро вращающегося волчка, разумеется, также подчиняется второму закону Ньютона. Именно поэтому ось волчка при любом воздействии на него посторонней силы всегда изменяет свое положение. Но такое изменение вследствие огромной разницы между силой, развивающейся в результате вращения, и «валящей» силой не заметно.

Таковы основные причины удивительного «поведения» волчка. Следует, однако, оговориться: целый ряд дополнительных причин остался не упомянутым, потому что дальнейшее углубление вопроса превратило бы большую часть нашей книжки в один из разделов теоретической механики. Поэтому мы ограничимся лишь сказанным.

Замечательные свойства быстро вращающегося волчка — вот в чем секрет устойчивости балерины, исполняющей фуэте. Этими же свойствами объясняются и поразительные манипуляции жонглера. Здесь мы видим умелое, однако безотчетное использование законов механики, законов вращения твердого тела вокруг неподвижной точки.

Где же еще, кроме эстрады и забавных детских игрушек, используются замечательные свойства волчка?

Изо дня в день, из века в век Солнце для нас, живущих на Земле, «восходит» и «заходит» в точно определенное для каждого дня и географического места время, «проходя» по точно определенному пути небосвода. Звезды на небе тоже «перемещаются» по строго определенным путям. Это видимое движение небесных тел является, прежде всего, следствием вращения Земли.

Предположим себе такой фантастический случай, когда наблюдатель находится в межзвездном пространстве против Северного полюса Земли. Отсюда он ясно видит точку воображаемой оси вращения, проходящей через полюс. Земля в течение суток, а точнее, за двадцать три часа пятьдесят шесть минут и четыре с одной десятой секунды, совершает один оборот, вращаясь против часовой стрелки.