Александр Краснов: Волчок и применение его свойств

Когда энергия, сообщенная при броске, иссякает, бумеранг, продолжая вращаться, начинает под действием силы тяжести падать.

Но и в этом случае быстро вращающийся бумеранг или шляпа из-за сопротивления воздуха не падает вертикально, а, скользя по воздуху, возвращается обратно.

Из этого примера мы убеждаемся, что шляпа и бумеранг устойчиво сохраняют свое положение в пространстве также вследствие вращения. Этот вывод подкрепляется еще более простым опытом с вареным куриным яйцом.

Как поставить куриное яйцо на заостренный конец, носок? Это можно сделать, лишь приведя яйцо в быстрое вращение. Вовсе не обязательно вращать его, поставив на носок. Лежащее на боку куриное яйцо, к нашему удивлению, при вращении вдруг «само по себе» встает на носок, сохраняя некоторое время это необычное положение.

Тела яйцеобразной формы подобны детской игрушке — волчку.

Неподвижный волчок также лишен устойчивости. Сколько бы мы ни пытались поставить его на заостренный конец, он будет безжизненно валиться на бок.

Совершенно иное происходит с быстро вращающимся волчком. Опираясь о поверхность своим острием и быстро вращаясь вокруг оси, волчок стоит будто «вкопанный» (рис. 5).

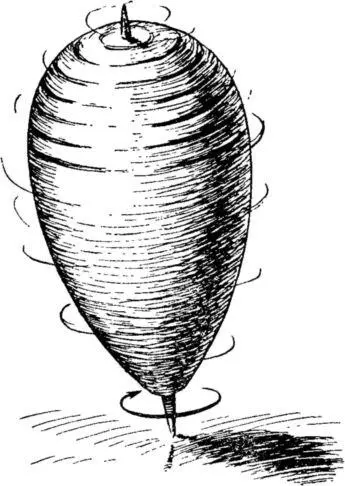
Рис. 5. Положение быстро вращающегося волчка.

Попытаемся свалить вращающийся волчок, толкнув его пальцем. Как это ни странно, он не упадет, а лишь отскочит в сторону, продолжая быстро вращаться.

Подбросив невращающийся волчок, мы увидим, что он беспорядочно переворачивается в воздухе. Приведем затем волчок в быстрое вращение на дощечке и подбросим его. Теперь он устойчиво сохраняет свое положение. Упав обратно, он по-прежнему продолжает вращаться. При этом наклон поверхности не изменит положения его оси. Волчок будет перемещаться под уклон, сохраняя свое вертикальное положение (рис. 6).

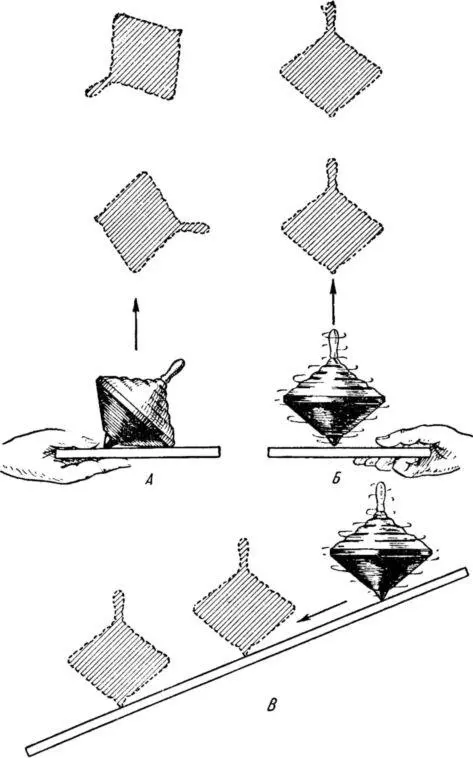
Рис. 6. Различные случаи «поведения волчка». А — невращающийся волчок, подброшенный, взлетает, беспорядочно кувыркаясь в пространстве; Б — быстро вращающийся волчок, подброшенный, устойчиво сохраняет свое положение в пространстве; В — на наклонной плоскости быстро вращающийся волчок легко «сбегает» под уклон, устойчиво сохраняя вертикальное положение своей оси в пространстве.

Вращающийся волчок замечателен прежде всего устойчивостью, то есть способностью неизменно сохранять вертикальное положение.

Но почему вращающиеся тела проявляют такую удивительную устойчивость?

К рассказу об этом мы и перейдем.

Удивительные свойства волчка издавна привлекали внимание многих ученых. Еще в XVIII веке делались попытки практически использовать эти свойства.

В механике волчком называют твердое тело, которое вращается около какой-то оси, имеющей неподвижную точку.

Математическое решение задачи о вращении твердого тела вокруг неподвижной точки представляет большую трудность и сложность. Полностью эта задача не решена и до настоящего времени.

Решить ее пытались многие ученые.

Вначале решение того или иного частного случая задачи, казалось бы, шло благополучно, но в итоге ничего не получалось. По этому поводу замечательная русская женщина, крупнейший ученый, Софья Васильевна Ковалевская говорила, что задача о вращении твердого тела может быть названа «математической русалкой».

Теоретическое решение задачи о вращении твердого тела осуществлено лишь для трех частных случаев. Окончательного, полного решения этого вопроса нет и поныне.

Решения трех частных случаев были выполнены в разное время крупнейшими учеными: членом Российской Академии наук Леонардом Эйлером, французским ученым Жозефом Луи Лагранжем и первой русской женщиной-ученым Софьей Ковалевской.

Л. Эйлер в своем знаменитом сочинении «Теория движения твердого тела» в 1765 г. дал решение задачи о движении вращающегося твердого тела, у которого центр тяжести (точка, через которую проходит сила тяжести тела при любых возможных положениях его) находится в точке опоры (рис. 7).

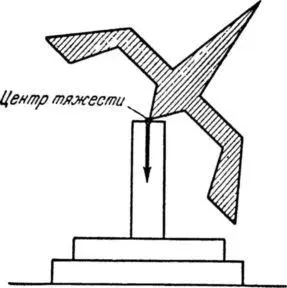
Рис. 7. Волчок, законы вращения которого открыл в XVIII веке член Российской Академии наук Леонард Эйлер.