Александр Краснов: Волчок и применение его свойств

Такой волчок, даже не вращаясь, сохраняет устойчивое равновесие.

Несколько позже Ж. Л. Лагранж (1736–1813 гг.) решил задачу более сложную, чем Л. Эйлер (рис. 8).

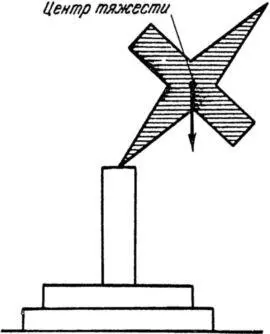
Рис. 8. Волчок, законы вращения которого открыл в конце XVIII и начале XIX века французский ученый Жозеф Луи Лагранж.

Он решил задачу вращения твердого тела, центр тяжести которого находится выше точки опоры.

Таким образом, труды Л. Эйлера и Ж. Л. Лагранжа были положены в основу теории «волчка». С тех пор многие ученые во всем мире пытались продолжить решение этой задачи. Однако на протяжении почти ста лет их попытки терпели неудачу. «Математическая русалка» не давалась ученым. Французская Академия наук установила специальную премию Бордена в размере трех тысяч франков лишь за усовершенствование решения этой задачи в «каком-либо существенном пункте».

Эта награда, вручаемая по конкурсу, долгое время не присуждалась никому; теоретические работы по «усовершенствованию в каком-либо существенном пункте» на рассмотрение не поступали. Так безуспешно прошли два конкурса.

По условиям конкурса следовало представить два пакета под одним и тем же названием (девизом). В одном из них должно было находиться решение задачи, а во втором — записка с именем представившего материал. Вначале вскрывали пакет с решением задачи, и специалисты давали заключение по нему. После этого вскрывали второй пакет, где была указана фамилия автора. Это исключало возможность пристрастной оценки.

В 1888 г. одна из пятнадцати работ, поступивших на третий конкурс, вызвала особенный восторг ученых, членов конкурсной комиссии. Эта работа значилась под девизом: «Говори, что знаешь, делай, что обязан, будь, чему быть».

Конкурсная комиссия, состоявшая из ряда крупнейших ученых, единодушно вынесла решение выдать автору этой работы премию, увеличенную с трех до пяти тысяч франков.

В отзыве о работе, заслужившей такое одобрение, между прочим, говорилось, что она является «замечательным трудом, который содержит открытие нового случая… автор не удовольствовался прибавлением решения к тем решениям, какие перешли к нам по этому предмету от Эйлера и Лагранжа, а сделал из своего открытия углубленное исследование с применением всех возможностей современной теории функций».

После этого, вскрыв второй конверт с девизом, комиссия узнала, что автором работы, получившей такое блестящее заключение, является Софья Васильевна Ковалевская.

Известный французский математик Дюбуа-Реймон, выступая на торжественном вручении премии, сказал: «Софья Ковалевская не только превзошла немногих предшественниц в математическом образовании, но заняла между современными математиками одно из самых видных мест. Она получила премию за решение вопроса о вращении твердого тела под влиянием действующих на него сил. Решение третьей задачи, самой сложной, принадлежит Ковалевской. Ее решением исчерпываются средства современного анализа».

Сложность задачи, решенной Софьей Ковалевской, нетрудно понять, если учесть, что у исследованного ею «волчка» центр тяжести находится где-то в стороне от точки опоры (рис. 9), а следовательно, вне оси вращения.

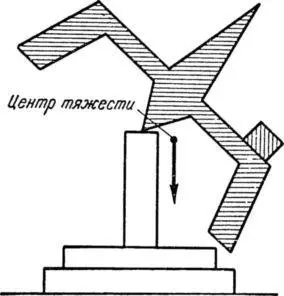
Рис. 9. Самый сложный случай быстро вращающегося волчка, законы движения которого открыла Софья Васильевна Ковалевская.

Движение такого волчка вокруг оси неравномерное, прерывистое.

Решение задачи, рассмотренной С. В. Ковалевской, чрезвычайно сложно. В математическом изложении его под силу разобраться только крупнейшим математикам, что подтверждается, например, такими фактами.

При вручении премии президент Французской Академии наук астроном Жансен говорил:

«Между венками, которые мы даем сегодня, один из прекраснейших и труднейших для достижения возлагается на чело женщины. Наши сочлены нашли, что труд ее является свидетельством не только глубокого и широкого знания, но и признаком ума великой изобретательности».

Высокое одобрение столь сложному труду С. В. Ковалевской дал старейший французский математик того времени Шарль Эрмит. Он писал Софье Васильевне, что с нетерпением ожидает опубликования ее трудов, чтобы заняться исследованием отдельных элементов этой работы, предполагая «собирать колосья со сжатого ею поля». Он надеялся путем исследования ее труда совершить ряд новых открытий.