Bruce Mesquita - Prediction - How to See and Shape the Future with Game Theory

Commitment problems come in other varieties. The classic game theory illustration of a commitment problem is seen in the game called the prisoner’s dilemma, which is played out on almost every cop show on TV every night of the week. The story is that two criminals (I’ll call them Chris and Pat) are arrested. Each is held in a separate cell, with no communication between them. The police and the DA do not have enough evidence to convict them of the serious crime they allegedly committed. But they do have enough evidence to convict them of a lesser offense. If Chris and Pat cooperate with each other by remaining silent, they’ll be charged and convicted of the lesser crime. If they both confess, they’ll each receive a stiff sentence. However, if one confesses and the other does not, then the one who confesses—ratting out the other—will get off with time served, and the other will be put away for life without a chance for parole.

It is possible, maybe even likely, that Chris and Pat, our two crooks, made a deal beforehand, promising to remain silent if they are caught. The problem is that their promise to each other is not credible because it’s always in their interest—if the game is not going to be repeated an indefinite number of times—to renege, talking a blue streak to make a deal with the prosecutor. Here’s how it works:

THE PRISONER’S DILEMMA

Pat’s Choices

→

Chris’s Choices

↓

Don’t confess (stay faithful to Chris)

Confess (rat out Chris)

Don’t confess (stay faithful to Pat)

Chris and Pat get 5 years

Chris gets life; Pat gets time served

Confess (rat out Pat)

Chris gets time served; Pat gets life

Chris and Pat get 15 years

After Chris and Pat are arrested, neither knows whether the other will confess or really will stay silent as promised. What Chris knows is that if Pat is true to his word and doesn’t talk, Chris can get off with time served by betraying Pat. If instead Chris stays faithful to her promise and keeps silent too, she can expect to get five years. Remember, game theory reasoning takes a dim view of human nature. Each of the crooks looks out for numero uno. Chris cares about Chris; Pat looks out only for Pat. So if Pat is a good, loyal buddy—that is, a sucker—Chris can take advantage of the chance she’s been given to enter a plea. Chris would walk and Pat would go to prison for life.

Of course, Pat works out this logic too, so maybe instead of staying silent, Pat decides to talk. Even then, Chris is better off confessing than she would be by keeping her mouth shut. If Pat confesses and Chris stays silent, Pat gets off easy—that’s neither here nor there as far as Chris is concerned—and Chris goes away for a long time, which is everything to her. If Chris talks too, her sentence is lighter than if she stayed silent while Pat confessed. Sure, Chris (and Pat) gets fifteen years, but Chris is young, and fifteen years, with a chance for parole, certainly beats life in prison with no chance for parole. In fact, whatever Chris thinks Pat will do, Chris’s best bet is to confess.

This produces the dilemma. If both crooks kept quiet they would each get a fairly light sentence and be better off than if both confessed (five years each versus fifteen). The problem is that neither one benefits from taking a chance, knowing that it’s always in the other guy’s interest to talk. As a consequence, Chris’s and Pat’s promises to each other notwithstanding, they can’t really commit to remaining silent when the police interrogate them separately.

IT’S ALL ABOUT THE DOG THAT DIDN’T BARK

The prisoner’s dilemma illustrates an application of John Nash’s greatest contribution to game theory. He developed a way to solve games. All subsequent, widely used solutions to games are offshoots of what he did. Nash defined a game’s equilibrium as the planned choice of actions—the strategy—of each player, requiring that the plan of action is designed so that no player has any incentive to take an action not included in the strategy. For instance, people won’t cooperate or coordinate with each other unless it is in their individual interest. No one in the game-theory world willingly takes a personal hit just to help someone else out. That means we all need to think about what others would do if we changed our plan of action. We need to sort out the “what ifs” that confront us.

Historians spend most of their time thinking about what happened in the world. They want to explain events by looking at the chain of things that they can observe in the historical record. Game theorists think about what did not happen and see the anticipated consequences of what didn’t happen as an important part of the cause of what did happen. The central characteristic of any game’s solution is that each and every player expects to be worse off by choosing differently from the way they did. They’ve pondered the counterfactual—what would my world look like if I did this or I did that?—and did whatever they believed would lead to the best result for them personally.

Remember the very beginning of this book, when we pondered why Leopold was such a good king in Belgium and such a monster in the Congo? This is part of the answer. The real Leopold would have loved to do whatever he wanted in Belgium, but he couldn’t. It was not in his interest to act like an absolute monarch when he wasn’t one. Doing some counterfactual reasoning, he surely could see that if he tried to act like an absolute ruler in Belgium, the people probably would put someone else on the throne or get rid of the monarchy altogether, and that would be worse for him than being a constitutional monarch. Seeing that prospect, he did good works at home, kept his job, and freed himself to pursue his deepest interests elsewhere. Not facing such limitations in the Congo, there he did whatever he wanted.

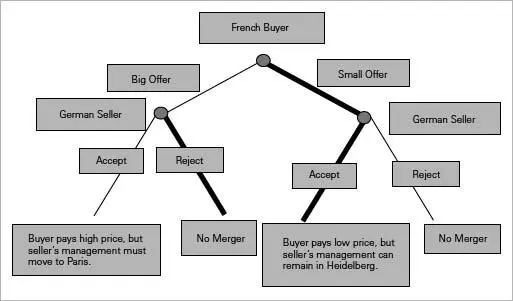
This counterfactual thinking becomes especially clear if we look at a problem or game as a sequence of moves. In the prisoner’s dilemma table I showed what happens when the two players choose without knowing what the other will do. Another way to see how games are played is to draw a tree that shows the order in which players make their moves. Who gets to move first matters a lot in many situations, but it does not matter in the prisoner’s dilemma because each player’s best choice of action is the same—confess—whatever the other crook does. Let’s have a look at a prospective corporate acquisition I worked on (with the details masked to maintain confidentiality). In this game, anticipating what the other player will do is crucial to getting a good outcome.

The buyer, a Paris-based bank, wanted to acquire a German bank. The buyer was prepared to pay a big premium for the German firm but was insistent on moving all of the German executives to the corporate headquarters in Paris. As we analyzed the prospect of the acquisition, it became apparent that the price paid was not the decisive element for the Heidelberg-based bank. Sure, everyone wanted the best price they could get, but the Germans loved living in Heidelberg and were not willing to move to Paris just for money. Paris was not for them. Had the French bankers pushed ahead with the offer they had in mind, the deal would have been rejected, as can be seen in the game tree below. But because their attention was drawn to the importance the Germans attached to where they lived, the offer was changed from big money to a more modest amount—fine enough for the French—but with assurances that the German executives could remain in Heidelberg for at least five years, which wasn’t ideal for the French, but necessary for their ends to be realized.

FIG. 3.1. Pay Less to Buy a Bank