Неизвестно - Prolog

Преимущество упорядочивания состоит в том, что для поиска некоторого объекта в двоичном справочнике всегда достаточно просмотреть не более одного поддерева. Экономия при поиске объекта Х достигается за счет того, что, сравнив Х с корнем, мы можем сразу же отбросить одно из поддеревьев. Например, пусть мы ищем элемент 6 в дереве, изображенной на рис. 9.6. Мы начинаем с корня 5, сравниваем 6 с 5, получаем 6 > 5. Поскольку все элементы данных в левом поддереве должны быть меньше, чем 5, единственная область, в которой еще осталась возможность найти элемент 6, - это правое поддерево. Продолжаем поиск в правом поддереве, переходя к вершине 8, и т.д.

Общий метод поиска в двоичном справочнике состоит в следующем:

Для того, чтобы найти элемент Х в справочнике Д, необходимо:

если Х - это корень справочника Д, то считать, что Х уже найден, иначе

если Х меньше, чем корень, то искать Х в левом поддереве, иначе

искать Х в правом поддереве;

если справочник Д пуст, то поиск терпит неудачу.

Эти правила запрограммированы в виде процедуры, показанной на рис. 9.7. Отношение больше( X, Y), означает, что Х больше, чем Y. Если элементы, хранимые в дереве, - это числа, то под "больше, чем" имеется в виду просто Х > Y.

Существует способ использовать процедуру внутритакже и для построения двоичного справочника. Например, справочник Д, содержащий элементы 5, 3, 8, будет построен при помощи следующей последовательности целей:

?- внутри( 5, Д), внутри( 3, Д), внутри( 8, Д).

Д = дер( дер( Д1, 3, Д2), 5, дер( Д3, 8, Д4) ).

Переменные Д1, Д2, Д3 и Д4 соответствуют четырем неопределенным поддеревьям. Какими бы они ни были, все равно дерево Д будет содержать заданные элементы 3, 5 и 8. Структура построенного дерева зависит от того порядка, в котором указываются цели (рис. 9.8).

внутри( X, дер( _, X, _ ).

внутри( X, дер( Лев, Корень, Прав) ) :-

больше( Корень, X), % Корень больше, чем Х

внутри( X, Лев). % Поиск в левом поддереве

внутри( X, дер( Лев, Корень, Прав) ) :-

больше( X, Корень), % Х больше, чем корень

внутри( X, Прав). % Поиск в правом поддереве

Рис. 9. 7. Поиск элемента Х в двоичном справочнике.

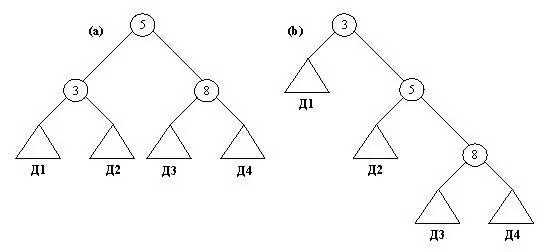
Рис. 9. 8. (а) Дерево Д, построенное как результат достижения целей: внутри( 5, Д), внутри( 3, Д), внутри( 8, Д). (b) Дерево, полученное при другом порядке целей: внутри( 5, Д), внутри( 3, Д), внутри( 8, Д).

Здесь уместно сделать несколько замечаний относительно эффективности поиска в справочниках. Вообще говоря, поиск элемента в справочнике эффективнее, чем поиск в списке. Но насколько? Пусть n - число элементов множества. Если множество представлено списком, то ожидаемое время поиска будет пропорционально его длине n . В среднем нам придется просмотреть примерно половину списка. Если множество представлено двоичным деревом, то время поиска будет пропорционально глубине дерева. Глубина дерева - это длина самого длинного пути между корнем и листом дерева. Однако следует помнить, что глубина дерева зависит от его формы

.

Мы говорим, что дерево (приближенно) сбалансировано, если для каждой вершины дерева соответствующие два поддерева содержат примерно равное число элементов. Если дерево хорошо сбалансировано, то его глубина пропорциональна log n . В этом случае мы говорим, что дерево имеет логарифмическую сложность. Сбалансированный справочник лучше списка настолько же, насколько log n меньше n . К сожалению, это верно только для приближенно сбалансированного дерева. Если происходит разбалансировка дерева, то производительность падает. В случае полностью разбалансированных деревьев, дерево фактически превращается в список. Глубина дерева в этом случае равна n , а производительность поиска оказывается столь же низкой, как и в случае списка. В связи с этим мы всегда заинтересованы в том, чтобы справочники были сбалансированы. Методы достижения этой цели мы обсудим в гл. 10.

Упражнения

9. 9. Определите предикаты

двдерево( Объект)

справочник( Объект)

распознающие, является ли Объектдвоичным деревом или двоичным справочником соответственно. Используйте обозначения, введенные в данном разделе.