Неизвестно - Prolog

Используйте в качестве вспомогательных следующие отношения:

означает( 0, нуль).

означает( 1, один).

означает( 2, два).

. . .

Посмотреть ответ

3. 8. Определите отношение

подмножество( Множество, Подмножество)

где Множествои Подмножество- два списка представляющие два множества. Желательно иметь возможность использовать это отношение не только для проверки включения одного множества в другое, но и для порождения всех возможных подмножеств заданного множества. Например:

?- подмножество( [а, b, с], S ).

S = [a, b, c];

S = [b, c];

S = [c];

S = [ ];

S = [a, c];

S = [a];

. . .

Посмотреть ответ

3. 9. Определите отношение

разбиениесписка( Список, Список1, Список2)

так, чтобы оно распределяло элементы списка между двумя списками Список1и Список2и чтобы эти списки были примерно одинаковой длины. Например:

разбиениесписка( [а, b, с, d, e], [a, с, е], [b, d]).

Посмотреть ответ

3. 10. Перепишите программу об обезьяне и бананах из главы 2 таким образом, чтобы отношение

можетзавладеть( Состояние, Действия)

давало не только положительный или отрицательный ответ, но и порождало последовательность действий обезьяны, приводящую ее к успеху. Пусть Действиябудет такой последовательностью, представленной в виде списка ходов:

Действия = [ перейти( дверь, окно),

передвинуть( окно, середина),

залезть, схватить ]

Посмотреть ответ

3. 11. Определите отношение

линеаризация( Список, ЛинейныйСписок)

где Списокможет быть списком списков, а ЛинейныйСписок- это тот же список, но "выровненный" таким образом, что элементы его подсписков составляют один линейный список. Например:

? - линеаризация( [а, d, [с, d], [ ], [[[е]]], f, L).

L = [a, b, c, d, e, f]

Посмотреть ответ

Назад | Содержание | Вперёд

Назад | Содержание | Вперёд

3. 3. Операторная запись (нотация)

В математике мы привыкли записывать выражения в таком виде:

2*a + b*с

где + и * - это операторы, а 2 , а , b , с - аргументы. В частности, + и * называют инфиксными операторами, поскольку они появляются между своими аргументами. Такие выражения могут быть

представлены в виде деревьев, как это сделано на рис. 3.6, и

записаны как прологовские термы

с

+

и

*

в качестве функторов:

+( *( 2, а), *( b, с) )

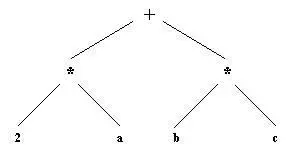
Рис. 3. 6. Представление выражения 2*а+b*с в виде дерева.

Поскольку мы обычно предпочитаем записывать такие выражения в привычной инфиксной форме операторов, Пролог обеспечивает такое удобство. Поэтому наше выражение, записанное просто как

2*а + b*с

будет воспринято правильно. Однако это лишь внешнее представление объекта, которое будет автоматически преобразовано в обычную форму прологовских термов. Такой терм выводится пользователю снова в своей внешней инфиксной форме.

Выражения рассматриваются Прологом просто как дополнительный способ записи, при котором не вводятся какие-либо новые принципы структуризации объектов данных. Если мы напишем а + b, Пролог поймет эту запись, как если бы написали +(а, b). Для того, чтобы Пролог правильно воспринимал выражения типа а + b*с, он должен знать, что *связывает сильнее, чем +. Будем говорить, что + имеет более низкий приоритет, чем *. Поэтому верная интерпретация выражений зависит от приоритетов операторов. Например, выражение а + b*с, в принципе можно понимать и как

+( а, *( b, с) )

и как

*( +( а, b), с

)

Общее правило состоит в том, что оператор с самым низким приоритетом расценивается как главный функтор терма. Если мы хотим, чтобы выражения, содержащие + и *, понимались в соответствии с обычными соглашениями, то + должен иметь более низкий приоритет, чем *. Тогда выражение а + b*созначает то же, что и а + (b*с). Если имеется в виду другая интерпретация, то это надо указать явно с помощью скобок, например ( а+b)*с.

Программист может вводить свои собственные операторы. Так, например, можно определить атомы имеети поддерживаетв качестве инфиксных операторов, а затем записывать в программе факты вида: