Неизвестно - Prolog

V( P, Альфа, Бета) <= Альфа если V( P) <= Альфа

V( P, Альфа, Бета) = V( P) если Альфа < V( P) < Бета

V( P, Альфа, Бета) >= Бета если V( P) >= Бета

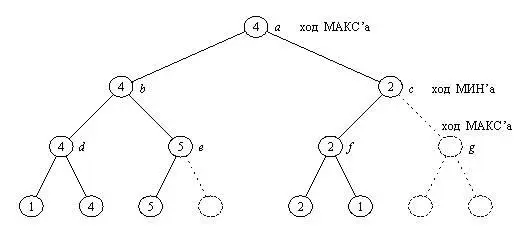
Рис. 15. 4. Дерево рис. 15.2 после применения альфа-бета алгоритма.

Пунктиром показаны ветви, отсеченные альфа-бета алгоритмом

для экономии времени поиска. В результате некоторые из

рабочих оценок стали приближенными (вершины c , е , f ;

сравните с рис.15.2). Однако этих приближенных оценок

достаточно для вычисления точной оценки корневой

вершины и построения основного варианта.

Очевидно, что, умея вычислять "достаточно хорошую" оценку, мы всегда можем вычислить точную оценку корневой позиции Р , установив границы интервала следующим образом:

V( Р, -бесконечность, +бесконечность) = V( P)

На рис. 15.5 показана реализация альфа-бета алгоритма в виде программы на Прологе. Здесь основное отношение -

альфабета( Поз, Альфа, Бета, ХорПоз, Оц)

где ХорПоз- преемник позиции Позс "достаточно хорошей" оценкой Оц, удовлетворяющей всем указанным выше ограничениям:

Оц = V( Поз, Альфа, Бета)

Процедура

прибл_лучш( СписПоз, Альфа, Бета, ХорПоз, Оц)

находит достаточно хорошую позицию ХорПозв списке позиций СписПоз; Оц- приближенная (по отношению к Альфаи Бета) рабочая оценка позиции ХорПоз.

Интервал между Альфа и Бета может сужаться (но не расширяться!) по мере углубления поиска, происходящего при рекурсивных обращениях к альфа-бета процедуре. Отношение

нов_границы( Альфа, Бета, Поз, Оц, НовАльфа, НовБета)

определяет новый интервал (НовАльфа, НовБета). Он всегда уже, чем старый интервал (Альфа, Бета), или равен ему. Таким образом, чем глубже мы оказываемся в дереве поиска, тем сильнее проявляется тенденция к сжатию интервала Альфа-Бета , и в результате оценивание позиций на более глубоких уровнях происходит в условиях более тесных границ. При более узких интервалах допускается большая степень "приблизительности" при вычислении оценок, а следовательно, происходит больше отсечений ветвей дерева. Возникает интересный вопрос: насколько велика экономия, достигаемая альфа-бета алгоритмом по сравнению с программой минимаксного полного перебора

рис. 15.3?

Эффективность альфа-бета процедуры зависит от порядка, в котором просматриваются позиции. Всегда лучше первыми рассматривать самые сильные ходы с каждой из сторон. Легко показать на примерах, что

% Альфа-бета алгоритм

альфабета( Поз, Альфа, Бета, ХорПоз, Оц) :-

ходы( Поз, СписПоз), !,

прибл_лучш( СписПоз, Альфа, Бета, ХорПоз, Оц);

стат_оц( Поз, Оц).

прибл_лучш( [Поз | СписПоз], Альфа, Бета, ХорПоз, ХорОц) :-

альфабета( Поз, Альфа, Бета, _, Оц),

дост_хор( СписПоз, Альфа, Бета, Поз, Оц, ХорПоз, ХорОц).

дост_хор( [ ], _, _, Поз, Оц, Поз, Оц) :- !.

% Больше нет кандидатов

дост_хор( _, Альфа, Бета, Поз, Оц, Поз, Оц) :-

ход_мина( Поз), Оц > Бета, !;

% Переход через верхнюю границу

ход_макса( Поз), Оц < Альфа, !.

% Переход через нижнюю границу

дост_хор( СписПоз, Альфа, Бета, Поз, Оц, ХорПоз, ХорОц) :-

нов_границы( Альфа, Бета, Поз, Оц, НовАльфа, НовБета),

% Уточнить границы

прибл_лучш( СписПоз, НовАльфа, НовБета, Поз1, Оц1),

выбор( Поз, Оц, Поз1, Оц1, ХорПоз, ХорОц).

нов_границы( Альфа, Бета, Поз, Оц, Оц, Бета) :-

ход_мина( Поз), Оц > Альфа, !.

% Увеличение нижней границы

нов_границы( Альфа, Бета, Поз, Оц, Альфа, Оц) :-

ход_макса( Поз), Оц < Бета, !.

% Уменьшение верхней границы

нов_границы( Альфа, Бета, _, _, Альфа, Бета).

выбор( Поз, Оц, Поз1, Оц1, Поз, Оц) :-

ход_мина( Поз), Оц > Оц1, !;

ход_макса( Поз), Оц < Оц1, !.

выбор( _, _, Поз1, Оц1, Поз1, Оц1).

Рис. 15. 5. Реализация альфа-бета алгоритма.

возможен настолько неудачный порядок просмотра, что альфа-бета алгоритму придется пройти через все вершины, которые просматривались минимаксным алгоритмом полного перебора. Это означает, что в худшем случае альфа-бета алгоритм не будет иметь никаких преимуществ. Однако, если порядок просмотра окажется удачным, то экономия может быть значительной. Пусть N - число терминальных поисковых позиций, для которых вычислялись статические оценки алгоритмом минимаксного полного перебора. Было доказано, что в лучшем случае, когда самые сильные ходы всегда рассматриваются первыми, альфа-бета алгоритм вычисляет статические оценки только для N позиций.