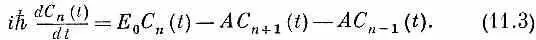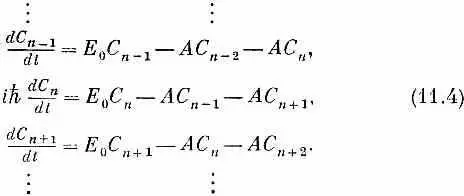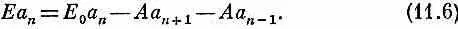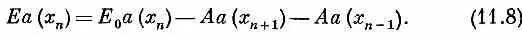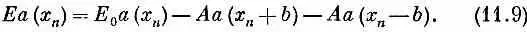Feynmann - Feynmann 9

Изменим на время обозначения, и амплитуду < n |j>, свя­занную с n -м атомом, обозначим через С n . Тогда (11.1) будет иметь вид

Если бы вы знали каждую из амплитуд С n в данный момент, то, взяв квадраты их модулей, можно было бы получить вероят­ность того, что вы увидите электрон, взглянув в этот момент на атом п.

Но что сталось бы чуть позже? По аналогии с изученными нами системами с двумя состояниями мы предлагаем составить гамильтоновы уравнения для этой системы в виде уравнений такого типа:

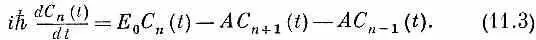
Первый справа коэффициент Е 0 физически означает энергию, которую имел бы электрон, если бы он не мог просачиваться от одного атома к другим. (Совершенно неважно, что мы назовем , Е 0 ; мы неоднократно видели, что реально это не означает ничего, кроме выбора нуля энергии.) Следующий член представляет амплитуду в единицу времени того, что электрон из ( n +1)-й ямки просочится в n -ю ямку, а последний член означает ампли­туду просачивания из ( n -1)-й ямки. Как обычно, А считается постоянным (не зависящим от t ).

Для полного описания поведения любого состояния |j> надо для каждой из амплитуд С n иметь по одному уравнению типа (11.3). Поскольку мы намерены рассмотреть кристалл с очень большим количеством атомов, то допустим, что состоя­ний имеется бесконечно много, атомы тянутся без конца в обе стороны. (При конечном числе атомов придется специально обращать внимание на то, что случается на концах.) А если ко­личество N наших базисных состояний бесконечно велико, то и вся система наших гамильтоновых уравнений бесконечна! Мы напишем только часть ее:

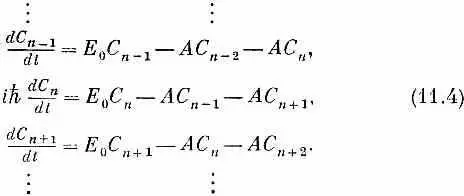
§ 2. Состояния определенной энергии

Об электроне в решетке мы теперь уже можем узнать очень многое. Для начала попробуем отыскать состояния определен­ной энергии. Как мы видели в предыдущих главах, это означает, что надо отыскать такой случай, когда все амплитуды меняются с одной частотой, если только они вообще меняются. Мы ищем решение в виде

Комплексное число а n говорит нам о том, какова не зависящая от времени часть амплитуды того, что электроны будут об­наружены возле n -го атома. Если это пробное решение подставить для проверки в уравнения (11.4), то получим

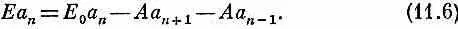
Перед нами бесконечное число уравнений для бесконечного количества неизвестных а n ! Ситуация тяжелая!

Но мы знаем, что надо только взять детерминант... нет, по­годите! Детерминанты хороши, когда уравнений два, три или четыре. Но здесь их очень много, даже бесконечно много, и вряд ли от детерминантов будет толк. Нет, лучше попробовать решать эти уравнения прямо. Во-первых, пронумеруем положения атомов; будем считать, что n - й атом находится в х n , а ( n + 1)-й— в х n + 1 . Если расстояние между атомами равно b (как на фиг. 11.1), то х n + 1 =х n + b . Взяв начало координат в атоме номер нуль, можно даже получить х n = nb . Уравнение (11.5) можно тогда переписать в виде

а уравнение (11.6) превратится в

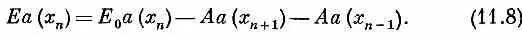
Пользуясь тем, что x n + 1 = x n + b , это выражение можно также записать в виде

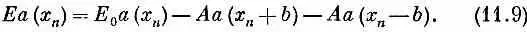
Это уравнение немного походит на дифференциальное. Оно говорит, что величина а(х) в точке х n связана с той же физиче­ской величиной в соседних точках х n ± b . (Дифференциальное уравнение связывает значения функции в точке с ее значениями в бесконечно близких точках.) Может быть, здесь подойдут методы, которыми мы обычно пользуемся для решения диффе­ренциальных уравнений? Попробуем.