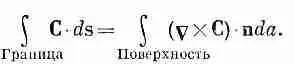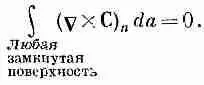
ранее. Получается новая теорема:
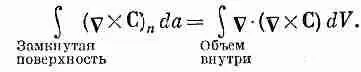
Это нас должно заинтересовать, потому что у нас уже есть одна теорема о поверхностном интеграле векторного поля. Такой поверхностный интеграл равен объемному интегралу от дивергенции вектора, как это следует из теоремы Гаусса [уравнение (3.18)]. Теорема Гаусса в применении к СXС утверждает, что
(3.40)
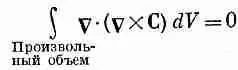
Мы заключаем, что интеграл в правой части должен обращаться в нуль и что это должно быть справедливо для любого векторного поля С, каким бы оно ни было.
(3.41)
Раз уравнение (3.41) выполнено для произвольного объема, то в каждой точке пространства подынтегральное выражение должно быть равно нулю. Получается, что
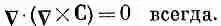
Тот же результат был выведен с помощью векторной алгебры в гл. 2, § 7. Теперь мы начинаем понимать, как все здесь прилажено одно к другому.
§ 8. Итоги
Подытожим теперь все, что мы узнали о векторном исчислении. Вот самые существенные моменты гл. 2 и 3.
1. Операторы д/дх, д/ду и д / dz можно рассматривать как три составляющих векторного оператора С ; формулы, следующие из векторной алгебры, остаются правильными, если этот оператор считать вектором
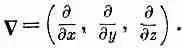
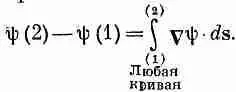
2. Разность значений скалярного поля в двух точках равна криволинейному интегралу от касательной составляющей градиента этого скаляра вдоль любой кривой, соединяющей первую точку со второй:
(3.42)
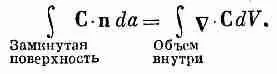 Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности равен интегралу от дивергенции вектора по объему, лежащему внутри этой поверхности:
Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности равен интегралу от дивергенции вектора по объему, лежащему внутри этой поверхности:
(3.43)
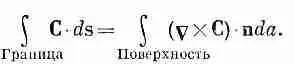
4. Криволинейный интеграл от касательной составляющей произвольного вектора по замкнутому контуру равен поверхностному интегралу от нормальной составляющей ротора этого вектора по произвольной поверхности, ограниченной этим контуром
(3.44)
От редактора. Начиная изучать уравнения Максвелла, обратите внимание, что в этих лекциях используется рационализированная система единиц, в которой уравнения Максвелла не содержат коэффициентов.
Более привычно вместо e 0 писать e 0 /4 p ; тогда коэффициент 4 p исчезает из знаменателя закона Кулона (4.9), но появляется в правых частях уравнений (4.1) и (4.3). [Улучшение системы единиц всегда похоже на Тришкин кафтан.]
Кроме того, вместо квадрата скорости света вводят новую постоянную m 0 = e 0 / c 2 , называют ее (довольно неудачно) магнитной проницаемостью пустоты (так же, как e 0 называют диэлектрической проницаемостью пустоты) и обозначают e 0 E = D , B = m 0 H .
Будьте осторожны! Проверяйте систему единиц, когда открываете новую книгу об электричестве!
*Конечно, последующие выкладки в равной мере относятся и к любому прямоугольному параллелепипеду.
Глава 4
ЭЛЕКТРОСТАТИКА
§1. Статика
§2.Закон Кулона; наложение сил
§З. Электрический потенциал
§4. E=- ▽ φ
§5.Поток поля Е
§6.Закон Гаусса; дивергенция поля Е
§7 .Поле заряженного шара
Читать дальше

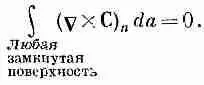
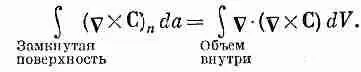
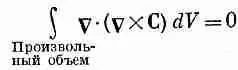
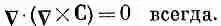
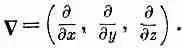
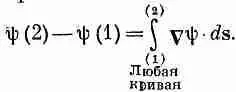
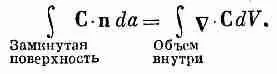 Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности равен интегралу от дивергенции вектора по объему, лежащему внутри этой поверхности:
Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности равен интегралу от дивергенции вектора по объему, лежащему внутри этой поверхности: