Feynmann - Feynmann 3

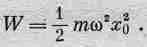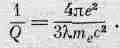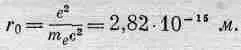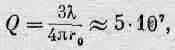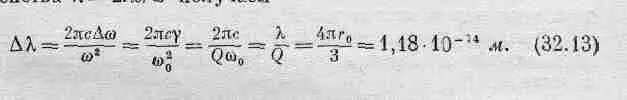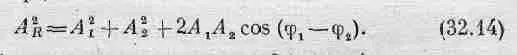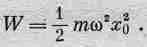
А что нужно взять в качестве энергии W осциллятора? Кине­тическая энергия осциллятора равна 1/2mv 2, а средняя кинети­ческая энергия равна mш 2x20/4. Но мы помним, что полная энер­гия осциллятора равна средней кинетической плюс средняя потенциальная, причем обе они для осциллятора равны; поэтому полная энергия равна

(32.9)

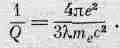
Какую частоту следует подставить в наши формулы? Мы возь­мем собственную частоту w 0, потому что практически это и есть частота излучения атома, а вместо m подставим m e . После ряда сокращений эта формула приводится к виду

(32.10)

(Для большей ясности и из соображений близости к исторически принятой форме мы ввели величину е 2= q 2 e/4pe 0и записали 2p/l вместо w 0/с.) Поскольку величина Q безразмерна, множи­тель е 2/m ес 2, зависящий только от массы и заряда электрона и выражающий его внутренние свойства, обязан иметь размер­ность длины. Он был назван классическим радиусом электрона, потому что в старых моделях электрона радиационное сопротив­ление пытались объяснить действием одной части электрона на другие его части, для чего размеры электрона приходилось вы­бирать порядка e 2/m ec 2. Но эта величина потеряла свой прежний смысл, и никто теперь не считает, что электрон имеет такой

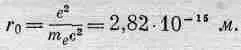
радиус. Численное значение классического радиуса электрона следующее:

(32.11)

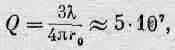
Вычислим теперь значение Q для атома, излучающего ви­димый свет, например для атома натрия. Длина волны излу­чения натрия равна примерно 6000 Е и находится в желтой части спектра; эта величина довольно типична. Отсюда

(32.12)

т. е. для атомов Q порядка 10 8. Это значит, что атомный осциллятор колеблется 10 8 рад, или примерно 10 7периодов, прежде чем его энергия уменьшится в 1 /е раз. Частота колебаний света v = с/ l при длине волны 6000 Е составляет 10 15 гц, а, следовательно, время жизни, т. е. время, за которое энер­гия уменьшится в Не раз, есть величина порядка 10 -8сек.

Примерно за такое же время высвечиваются свободные атомы в обычных условиях. Проведенная оценка справедлива только для атомов в пустом пространстве, не подверженных никаким внешним воздействиям. Если электрон находится в твердом теле, он сталкивается с другими атомами и электро­нами, и тогда возникает добавочное сопротивление и затухание будет другим.

Величина эффективного сопротивления у, определяющая сопротивление осциллятора, может быть найдена из соотноше­ния 1/ Q = g/w o; вспомним, что именно y определяет ширину резо­нансной кривой (см. фиг. 23.2) . Итак, мы вычислили шири­ны спектральных линий для свободно излучающих атомов! Из равенства l=2pc/w получаем

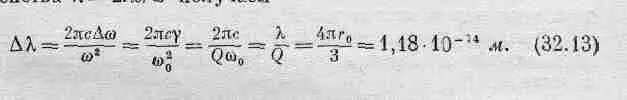
§ 4. Независимые источники

Прежде чем перейти ко второй теме этой главы — рассея­нию света, обсудим частный случай явления интерференции, который мы до сих пор не рассматривали. Речь пойдет о таком случае, когда интерференция не возникает. Пусть имеются два источника S 1и S 2с амплитудами поля a 1и A 2. Излучение регистрируется в некоторой точке, в которую оба луча приходят с фазами j 1и j 2(фазы зависят от истинного момента излучения и времени запаздывания, являющегося функцией точки на­блюдения).

Наблюдаемая интенсивность излучения получается сложе­нием двух комплексных векторов с модулями a 1и A 2и фазами j 1и j 2(как в гл. 30) и возведением в квадрат; таким образом, энергия пропорциональна

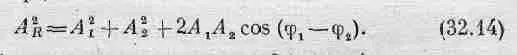
Если бы не было перекрестного члена 2A 1A 2cos(j 1-j 2), пол­ная энергия в данном направлении была бы равна сумме энер­гий A 1 2+A 2 2; излучаемых по отдельности каждым источником, что соответствует нашим обычным представлениям. Иначе говоря, интенсивность света, падающего на предмет от двух источников, совпала бы с суммой интенсивностей обоих источ­ников. С другой стороны, если оставить перекрестный член, суммы интенсивностей не получится, потому что возникнет ин­терференция. В тех случаях, когда перекрестный член роли не играет, интерференция, казалось бы, отсутствует. Фактически же она возникает всегда, но подчас ее не удается наблюдать.