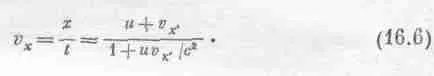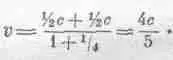Feynmann - Feynmann 2

Теперь займемся интересным вопросом о сложении скоростей в теории относительности. Напомним, что первоначально загадка состояла в том, что свет проходит 300 000 км/сек во всех системах, даже если они движутся друг относительно друга. Это — частный случай более общей задачи. Приведем пример. Пусть предмет внутри космического корабля движется вперед со скоростью 200 000 км/сек; скорость самого корабля тоже 200 000 км/сек. С какой скоростью перемещается предмет с точки зрения внешнего наблюдателя? Хочется сказать: 400 000 км/сек, но эта цифра уж больно подозрительна: полу­чается скорость большая, чем скорость света! Разве можно себе это представить?

Общая постановка задачи такова. Пусть скорость тела внутри корабля равна v (с точки зрения наблюдателя на корабле), а сам корабль имеет скорость и по отношению к Земле. Мы желаем знать, с какой скоростью v x это тело движется с точки зрения земного наблюдателя. Впрочем, это тоже не самый общий случай, потому что движение происходит в направ­лении х. Могут быть формулы для преобразования скоростей в направлении у или в любом другом; если они будут нужны, их всегда можно вывести. Внутри корабля скорость тела равна v x ' . Это значит, что перемещение х' равно скорости, умноженной на время:

x '= v x · ' t '. (16.3)

Остается только подсчитать, какие у тела значения х и t с точки зрения внешнего наблюдателя, если х' и t ' связаны соотношением (16.3). Подставим (16.3) в (16.2) и получим

Но здесь х выражено через t ' . А скорость с точки зрения внеш­него наблюдателя — это «его» расстояние, деленное на «его» время, а не на время другого наблюдателя ! Значит, надо и время подсчитать с его позиций

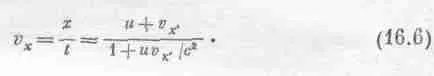
А теперь разделим х на t . Квадратные корни сократятся, останется же

Это и есть искомый закон: суммарная скорость не равна сумме скоростей (это привело бы ко всяким несообразностям), но «подправлена» знаменателем 1+uv/c 2.

Что же теперь будет получаться? Пусть ваша скорость внут­ри корабля равна половине скорости света, а скорость корабля тоже равна половине скорости света. Значит, и u равно 1/ 2 с, и v равно 1/ 2 c , но в знаменателе uv равно 1/ 4, так что

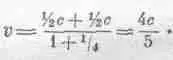
Выходит по теории относительности, что 1 / 2 и 1/ 2дают не 1 , a 4 / 5 . Небольшие скорости, конечно, можно складывать, как обычно, потому что, пока скорости по сравнению со скоростью света малы, о знаменателе (1 + uv / с 2 ) можно забыть, но на больших скоростях положение меняется.

Возьмем предельный случай. Положим, что человек на борту корабля наблюдает, как распространяется свет. Тогда v = c . Что обнаружит земной наблюдатель? Ответ будет такой:

Значит, если что-то движется со скоростью света внутри ко­рабля, то, с точки зрения стороннего наблюдателя, скорость не изменится, она по-прежнему будет равна скорости света! Это именно то, ради чего в первую очередь предназначал Эйн­штейн свою теорию относительности.

Конечно, бывает, что движение тела не совпадает по на­правлению с равномерным движением корабля. Например, тело движется «вверх» со скоростью v y 'по отношению к ко­раблю, а корабль движется «горизонтально». Проделывая такие же манипуляции (только х надо заменить на у), получаем

y = y '= v y ' t ', так что при v x '=0

Итак, боковая скорость тела уже не v y ' , a v y ' Ц (1- u 2 /с 2 ) . Этот результат мы получили, пользуясь формулами преобра­зований. Но он вытекает и прямо из принципа относительности по следующей причине (всегда бывает полезно докопаться до первоначальной причины). Мы уже раньше рассуждали (см. фиг. 15.3) о том, как могут работать движущиеся часы; свет ка­жется распространяющимся наискось со скоростью с в непо­движной системе, в то время как в движущейся системе он просто движется вертикально с той же скоростью. Мы нашли, что верти­кальная, компонента скорости в неподвижной системе меньше скорости света на множитель Ц(1-u 2/с 2) [см. уравнение (15.3)]. Пусть теперь материальная частица движется в тех же «часах» взад-вперед со скоростью, равной 1/n скорости света (фиг. 16.1).