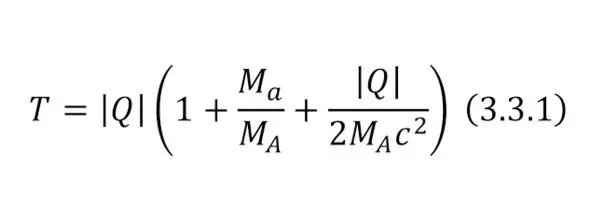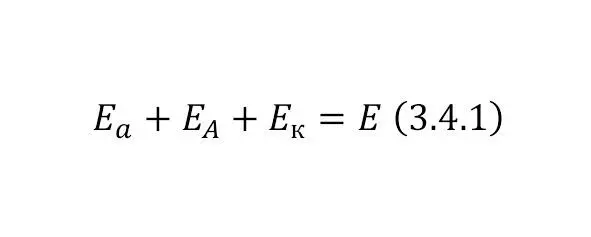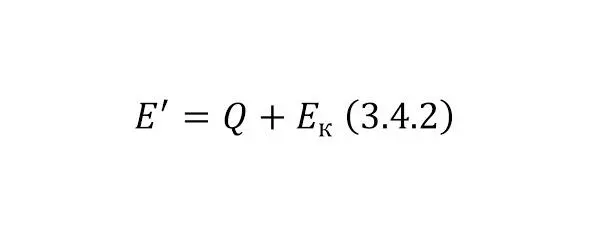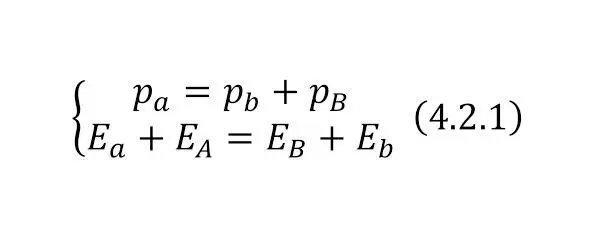Ибратжон Алиев - Программное моделирование явлений ядерных реакций на основе технологии создания множества данных с использованием системы алгоритмов на языке С++. Проект «Ядро-ЭВМ». Монография

Уже из данных операций и из указания всех истинных масс в коде (3.1.1) как действительный значений float, необходимо и выход ядерной реакции приводить в этом варианте. Этот факт также подтверждает аксиома из курса линейной алгебры, про принадлежность к одному множеству всех элементов, участвующих при выполнении некоторой алгебраической (арифметической) операции.

Кодовой записью этого случая является (Код 3.2.1).

Код 3.2.1. Запись кода выхода энергии реакции

float q4, t1, E1, E2;

q4= (a4+a5-a6-a7) *931.5;

cout <<���«Q="<<<" MeV»<

При этом для верного вывода также участвует и момент вывода единицы в МэВ. Единицы, которая выводится при произведении единицы в МэВ/ (а. е. м.), которым исчисляется элемент 931,5 и дефект масс исчисляемый также в единицах а. е. м.

Порог ядерной реакции определяется из равенства (3.3.1).

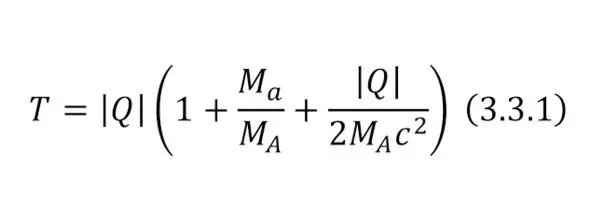
Из этого равенства определяем следующий код (3.3.1).

Код 3.3.1. Код по определению порога ядерной реакции

float q4, t1, E1, E2;

t1=abs (q4) * (1+a4/a5+abs (q4) / (2*a5*931.5));

cout <<���«T="<<<" MeV»<

При этом целочисленные данные является не только вещественными, но также эта формула является первой, в которой используется математическая операция (модуль или abs (a)), для выполнения которой необходимо использование и вызов математической библиотеки на первоначальной строке в виде кода 3.3.2.

Код 3.3.2. Код по вызову библиотеки математических операций

#include

Ещё одним элементом для дальнейших операций, необходим ввод понятия кинетической энергии влетающей частицы. Этот момент отделяется от предыдущего кода пустой строкой для понятия того, что это отдел ввода данных, а именно ввода кинетической энергии частицы.

Из этого уже исходят дополнительные 2 формулы, это общая энергия первой части и общая энергия выходная с кинетической (этот момент, также и объясняет, будет ли реакция вообще, если он больше нуля, то будет, если нет – нужно увеличивать кинетическую энергию). Необходимо привести эти уравнения (3.4.1—3.4.2).

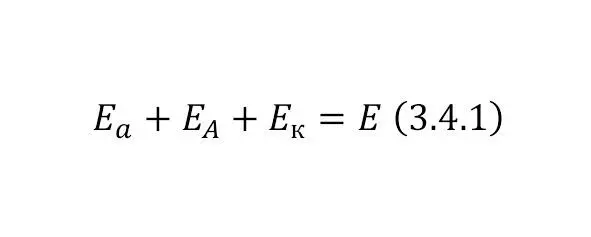
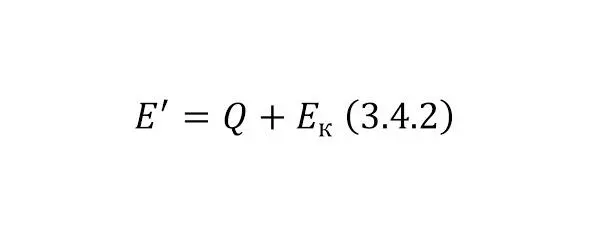
Эта часть кода, до этого момента описывается в (Коде 3.4.1).

Код 3.4.1. Общий код начиная с кинетической энергии до момента выходной общей энергии продуктов реакции

cout <<���«»<

cout <<���«Write Ek=»;

cin>> E1;

E2= (a4+a5) *931.5+E1;

cout <<���«»<

cout <<���«Ea+EA+Ek="<<

cout <<���«Energy: Q+Ek="<<

На этом моменте завершается условие для кинетической энергии.

Итого, был получен следующий код 3.5.1.

Код 3.5.1. Общий код на основе энергетических показателей

float q4, t1, E1, E2;

q4= (a4+a5-a6-a7) *931.5;

t1=abs (q4) * (1+a4/a5+abs (q4) / (2*a5*931.5));

cout <<���«Q="<<<" MeV»<

cout <<���«T="<<<" MeV»<

cout <<���«»<

cout <<���«Write Ek=»;

cin>> E1;

E2= (a4+a5) *931.5+E1;

cout <<���«»<

cout <<���«Ea+EA+Ek="<<

cout <<���«Energy: Q+Ek="<<

В самой же программе этот код выглядит следующим образом (Рис. 3.5.1).

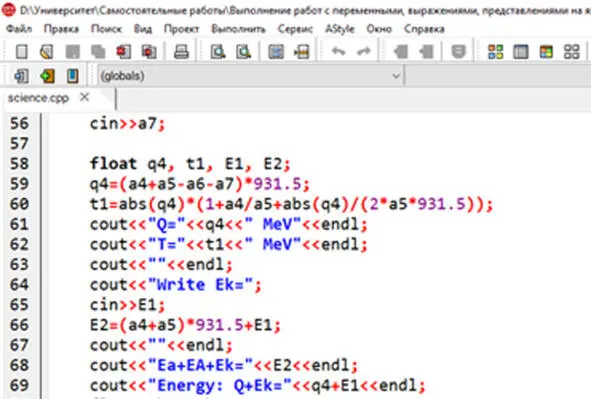
Рисунок 3.5.1. Общий код в самой программе

Для использования всесторонней достоверности при выведении и производстве математических, а также физических расчётов, необходимо учитывать релятивистский эффект, то есть моменты со всеми корнями, степенями и постоянными.

Из этого можно сделать вывод, что для использования в программном моделировании самого понятия релятивизма становится необходимым вызов математической библиотеки данных со всеми дополняющими функциями типа: pow (a,b), sqrt (a), lg (a), sin (x), cos (x), tan (x) и т. д.

Для определения распределения энергии продуктов ядерной реакции возможно привести решение системы уравнений вытекающей из (4.2.1).

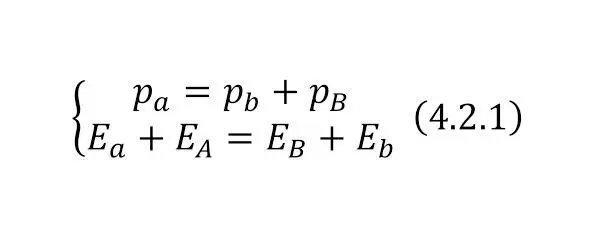
Но для начальной операции, как для простейшего случая возможно применение и двух уравнений (4.2.2) и (4.2.3).