Питер Макоуэн - Вычислительное мышление - Метод решения сложных задач

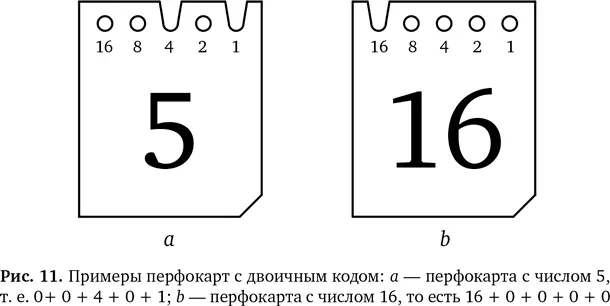
Какое отношения это имеет к нашим перфокартам? На них мы можем записывать числа в двоичной системе, используя отверстия для 0 и вырезы для 1. Чтобы записать на перфокарту число 5, начиная слева, нам нужно отверстие (0), еще отверстие (0), потом вырез (1), снова отверстие (0) и, наконец, вырез (1). Для числа 16 (10000) нам нужен один вырез и 4 отверстия. Если у нас есть место для пяти отверстий, мы можем записать на карту любое число до 31. Имея достаточно места (то есть достаточно степеней двойки и, соответственно, разрядов), мы можем записать любое число. Описанные примеры перфокарт приведены на рис. 11 аи 11 b.

Как только мы записали на карту число в двоичном коде в виде отверстий и вырезов, можно с легкостью найти любую карту. И здесь наступает черед метода «шиворот-навыворот».

Возьмите стопку карт и убедитесь, что они сложены срезанными уголками друг к другу, а отверстия выровнены в одну линию. Теперь вставьте карандаш в крайнее правое отверстие (колонку единиц) и стряхните все карты, у которых в этом месте вырез (как мы помним, это нечетные числа). У вас останутся только карты с 0. Теперь вернитесь к числу, которое вы хотите найти. Если в его двоичном коде в конце стоит 0, то сбросьтенижнюю стопку — те карты, которые вы стряхнули. Если в целевом числе там стоит 1, то оставьтенижнюю стопку. Повторите то же самое для каждого отверстия по очереди.

Например, мы ищем карту с номером 16. В двоичной системе это 10000. При движении слева направо выходит:

ВЫРЕЗ 1: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 2: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 4: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 8: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 16: 1 — ОСТАВЬТЕ упавшие карты.

Многократно сбрасывайте нижнюю стопку, пока, в пятом раунде, ее не нужно будет оставить. У вас останется карта с номером 16. Таким образом, прорабатывая двоичный код, можно найти любую карту. Попробуйте найти карту 5. В двоичной системе это 00101. При движении справа налево получаем:

ВЫРЕЗ 1: 1 — ОСТАВЬТЕ упавшие карты.

ВЫРЕЗ 2: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 4: 1 — ОСТАВЬТЕ упавшие карты.

ВЫРЕЗ 8: 0 — СБРОСЬТЕ упавшие карты.

ВЫРЕЗ 16: 0 — СБРОСЬТЕ упавшие карты.

У вас останется карта 5.

Оказывается, сбрасывая карты таким образом, вы поступаете как фокусник, сдающий карты по принципу «шиворот-навыворот». Чтобы это увидеть, нужно снова подключить логическое мышлениеи с его помощью найти точное объяснение происходящему.

Возьмите первый раунд, когда вы сбрасываете карты и одновременно ищете номер 16. Стряхнув первые перфокарты и затем избавившись от них, вы отметаете все карты с вырезом (1) в первой позиции двоичного числа. Это столбик единиц. У чисел 1, 3, 5, 7 будет вырез (1) в этой позиции — все это нечетные числа. Происходит то же самое, что и в первом раунде «шиворот-навыворот», когда мы сбрасываем каждую вторую карту. Как вы видели выше, мы переводим число из двоичной системы в десятичную, складывая числа в соответствующих разрядах (например, 5 = 4 + 0 + 1). Этот последний разряд единиц полностью определяет нечетные числа, в то время как все остальные — четные (2, 4, 8, 16, …).

Вот еще один способ понять, почему двоичное представление ведет к тому, что нечетные числа отбрасываются, — он поможет нам понять, как работает остальная часть фокуса. Подумайте, как мы считаем в двоичной системе: 0, 1, 2, 3, 4, … — это 000, 001, 010, 011, 100, … В колонке единиц во время счета значение меняется через раз, то есть в этой последней позиции по очереди оказываются 0, 1, 0, 1 — и так далее. Это значит, что если мы отбросим все единицы, то избавимся от каждой второй карты.

То есть мы показали, что в первом раунде происходит то же самое, что и в фокусе. Отбросив все карты с нечетными цифрами, мы переходим к следующему отверстию на перфокарте и, таким образом, к следующей позиции в двоичном числе. Эта операция убирает все числа, в составе которых есть разряд двоек. Например, это 6 (110 в двоичной системе), поскольку 6 = 4 + 2 + 0. На этот раз уходят 2 (10 в двоичной системе), 3 (11), 6 (110), 7 (111), 10 (1010), 11 (1011) и так далее. Однако нечетные числа уже были удалены, значит, на этот раз мы стряхнем 2, 6, 10, ... То есть остается каждая вторая карта. Это та же последовательность карт, которую мы удаляем во втором раунде «шиворот-навыворот».

Причина становится очевидной, если посмотреть на второй столбик в числах, записанных двоичным кодом. Там мы видим 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1 ...