В. н. широко практиковалось русской дореволюционной земской статистикой. Некоторые приёмы, в частности высоко оценённый В. И. Лениным многофазный отбор, не потеряли значения и до настоящего времени. ЦСУ СССР регулярно проводит обследование около 62 тыс. бюджетов семей рабочих, служащих и колхозников, а также ведёт единовременные обследования в разных областях социально-экономической статистики. Выборочным путём получена часть сведений при Всесоюзной переписи населения 1970. Выборочные обследования широко практикуются научными учреждениями, в частности при социологических исследованиях. Развивается и самостоятельная область В. н. — контроль качества промышленной продукции.
Лит.: Ковалевский А. Г., Основы теории выборочного метода, Саратов. 1924; Боярский А. Я., Старовский В. Н. [и др.], Теория математической статистики, М., 1930 и М., 1931; Юл Дж. Э. и Кендэл М. Дж., Теория статистики, пер. с англ., 14 изд., пересмотр, и расшир., М., 1960; Иойтс Ф., Выборочный метод в переписях и обследованиях, пер. с англ., М., 1965; Выборочное наблюдение в статистике СССР. Сб. статей под ред. А. Я. Боярского [и др.], М., 1966; Дружинин Н. К., Выборочный метод и его применение в социально-экономических исследованиях, М., 1970.
А. Г. Волков.
Вы'борочный ме'тод,статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку. Математическая теория В. м. опирается на два важных раздела математической статистики — теорию выбора из конечной совокупности и теорию выбора из бесконечной совокупности. Основное отличие В. м. для конечной и бесконечной совокупностей заключается в том, что в первом случае В. м. применяется, как правило, к объектам неслучайной, детерминированной природы (например, число дефектных изделий в данной партии готовой продукции не является случайной величиной: это число — неизвестная постоянная, которую и надлежит оценить по выборочным данным). Во втором случае В. м. обычно применяется для изучения свойств случайных объектов (например, для исследования свойств непрерывно распределённых случайных ошибок измерений, каждое из которых теоретически может быть истолковано как реализация одного из бесконечного множества возможных результатов).
Выбор из конечной совокупности и его теория являются основой статистических методов контроля качества и часто применяются в социологических исследованиях (см. Выборочное наблюдение ). Согласно теории вероятностей, выборка будет правильно отражать свойства всей совокупности, если выбор производится случайно, т. е. так, что любая из возможных выборок заданного объёма n из совокупности объёма N [число таких выборок равно N !/ n !( N — n )!] имеет одинаковую вероятность быть фактически выбранной.
На практике наиболее часто используется выбор без возвращения (бесповторная выборка), когда каждый отобранный объект перед выбором следующего объекта в исследуемую совокупность не возвращается (такой выбор применяется при статистическом контроле качества). Выбор с возвращением (выборка с повторением) рассматривается обычно лишь в теоретических исследованиях (примером выбора с возвращением является регистрация числа частиц, коснувшихся в течение данного времени стенок сосуда, внутри которого совершается броуновское движение ). Если n << N, то повторный и бесповторный выборы дают практически эквивалентные результаты.
Свойства совокупности, исследуемые В. м., могут быть качественными и количественными. В первом случае задача выборочного обследования заключается в определении количества М объектов совокупности, обладающих каким-либо признаком (например, при статистическом контроле часто интересуются количеством М дефектных изделий в партии объёма N ). Оценкой для М служит отношение m N/n , где m — число объектов с данным признаком в выборке объёма n . В случае количественного признака имеют дело с определением среднего значения совокупности 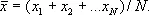 Оценкой для
Оценкой для 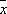 является выборочное среднее
является выборочное среднее 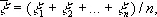 где x 1,..., x n— те значения из исследуемой совокупности x 1, x 2,..., x N , которые принадлежат выборке. С математической точки зрения 1-й случай — частная разновидность 2-го, которая имеет место, когда М величин x iравны 1, а остальные ( N — М ) равны 0; в этой ситуации
где x 1,..., x n— те значения из исследуемой совокупности x 1, x 2,..., x N , которые принадлежат выборке. С математической точки зрения 1-й случай — частная разновидность 2-го, которая имеет место, когда М величин x iравны 1, а остальные ( N — М ) равны 0; в этой ситуации 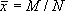 и
и 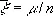 .
.
Читать дальше

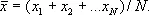 Оценкой для
Оценкой для 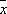 является выборочное среднее
является выборочное среднее 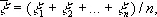 где x 1,..., x n— те значения из исследуемой совокупности x 1, x 2,..., x N , которые принадлежат выборке. С математической точки зрения 1-й случай — частная разновидность 2-го, которая имеет место, когда М величин x iравны 1, а остальные ( N — М ) равны 0; в этой ситуации
где x 1,..., x n— те значения из исследуемой совокупности x 1, x 2,..., x N , которые принадлежат выборке. С математической точки зрения 1-й случай — частная разновидность 2-го, которая имеет место, когда М величин x iравны 1, а остальные ( N — М ) равны 0; в этой ситуации 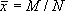 и
и 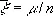 .
.