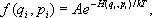
где H ( q i , p i ) — функция Гамильтона системы, т. е. её полная энергия, выраженная через координаты и импульсы частиц, k — Больцмана постоянная , Т — абсолютная температура; постоянная А не зависит от q i и p i и определяется из условия нормировки (сумма вероятностей пребывания системы во всех возможных состояниях должна равняться единице). Т. о., вероятность микросостояния определяется отношением энергии системы к величине kT (которая является мерой интенсивности теплового движения молекул) и не зависит от конкретных значений координат и импульсов частиц, реализующих данное значение энергии.
В квантовой статистике вероятность w n данного микроскопического состояния определяется значением энергетического уровня системы E п .
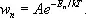
Для идеального газа, т. е. газа. в котором энергией взаимодействия частиц можно пренебречь, каноническое Г. р. переходит в Больцмана распределение, определяющее вероятность того, что координата и импульс (энергия) отдельной частицы имеют данные значения (см. Больцмана статистика ).
Если система изолирована, то её энергия постоянна; в этом случае справедливо микроканоническое Г. р., согласно которому все микроскопические состояния изолированной системы равновероятны. Микроканоническое Г. р. лежит в основе Г. р. канонического.
Лит . см. при статье Статистическая физика .
Г. Я. Мякишев.
Гиббса термодинамический потенциал
Ги'ббса термодинами'ческий потенциа'л, то же, что Гиббсова энергия ; см. также Потенциалы термодинамические .
Гиббси'т(по имени американского минералога Дж. Гиббса, G. Gibbs, 1776—1833), минерал; то же, что гидраргиллит .
Ги'ббсова эне'ргия, энергия Гиббса, изобарный потенциал, одна из характеристических функций термодинамической системы, обозначается G, определяется через энтальпию H, энтропию S и температуру Т равенством
G = H — TS . (1)
Г. э. является потенциалом термодинамическим . В изотермическом равновесном процессе, происходящем при постоянном давлении, убыль Г. э. данной системы равна полной работе, производимой системой в этом процессе, за вычетом работы против внешнего давления (т. е. равна максимальной полезной работе). Г. э. выражается обычно в кдж/моль или в ккал/моль . С помощью Г. э. и её производных могут быть в простой форме выражены др. термодинамические функции и свойства системы ( внутренняя энергия , энтальпия , химический потенциал и др.) в условиях постоянства температуры и давления. При этих условиях любой термодинамический процесс может протекать без затраты работы извне только в том направлении, которое отвечает уменьшению G ( dG < 0 ). Пределом протекания его без затраты работы, т. е. условием равновесия, служит достижение минимального значения G ( dG = 0, d 2G > 0 ). Г. э. широко используется при рассмотрении различных термодинамических процессов, проводимых при постоянных температуре и давлении. Через Г. э. определяется работа обратимого намагничивания магнетика и поляризации диэлектрика в этих условиях. Знание Г. э. важно для термодинамического рассмотрения фазовых переходов. Константа равновесия К а химической реакции при любой температуре Т определяется через стандартное изменение Г. э. DG° соотношением
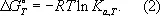
Широко используется Г. э. 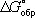 образования химического соединения, равная изменению Г. э. в реакции образования данного соединения (или простого вещества) из стандартного состояния соответствующих простых веществ. Для любой химической реакции
образования химического соединения, равная изменению Г. э. в реакции образования данного соединения (или простого вещества) из стандартного состояния соответствующих простых веществ. Для любой химической реакции 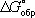 равна алгебраической сумме произведений
равна алгебраической сумме произведений 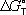 веществ, участвующих в реакции, на их коэффициенты в уравнении реакции. Для 298,15 К
веществ, участвующих в реакции, на их коэффициенты в уравнении реакции. Для 298,15 К 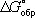 известны уже для нескольких тысяч веществ, что даёт возможность расчётным путём определять соответствующие значения
известны уже для нескольких тысяч веществ, что даёт возможность расчётным путём определять соответствующие значения 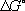 и К а для большого числа реакций.
и К а для большого числа реакций.
Читать дальше

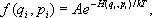
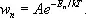
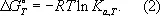
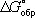 образования химического соединения, равная изменению Г. э. в реакции образования данного соединения (или простого вещества) из стандартного состояния соответствующих простых веществ. Для любой химической реакции
образования химического соединения, равная изменению Г. э. в реакции образования данного соединения (или простого вещества) из стандартного состояния соответствующих простых веществ. Для любой химической реакции 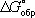 равна алгебраической сумме произведений
равна алгебраической сумме произведений 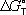 веществ, участвующих в реакции, на их коэффициенты в уравнении реакции. Для 298,15 К
веществ, участвующих в реакции, на их коэффициенты в уравнении реакции. Для 298,15 К 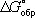 известны уже для нескольких тысяч веществ, что даёт возможность расчётным путём определять соответствующие значения
известны уже для нескольких тысяч веществ, что даёт возможность расчётным путём определять соответствующие значения 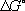 и К а для большого числа реакций.
и К а для большого числа реакций.