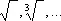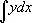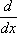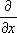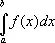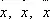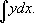БСЭ БСЭ - Большая Советская Энциклопедия (ЗН)

Дальнейшее развитие З. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики которого основа была уже в большой мере подготовлена в алгебре.

Даты возникновения некоторых математических знаков

знак	значение	Кто ввёл	Когда введён
Знаки индивидуальных объектов
¥	бесконечность	Дж. Валлис	1655
e'	основание натуральных логарифмов	Л. Эйлер	1736
p	отношение длины окружности к диаметру	У. Джонс Л. Эйлер	1706 1736
i	корень квадратный из -1	Л. Эйлер	1777 (в печати 1794)
i j k	единичные векторы, орты	У. Гамильтон	1853
П (а)	угол параллельности	Н.И. Лобачевский	1835
Знаки переменных объектов
x,y, z'	неизвестные или переменные величины	Р. Декарт	1637
r	вектор	О. Коши	1853
Знаки индивидуальных операций
+	сложение	немецкие математики	Конец 15 в.
–'	вычитание
´	умножение	У. Оутред	1631
×	умножение	Г. Лейбниц	1698
:	деление	Г. Лейбниц	1684
a 2, a 3,…, a n	степени	Р. Декарт	1637
	И. Ньютон	1676
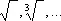	корни	К. Рудольф	1525
А. Жирар	1629
Log	логарифм	И. Кеплер	1624
log	Б. Кавальери	1632
sin	синус	Л. Эйлер	1748
cos	косинус
tg	тангенс	Л. Эйлер	1753
arc.sin	арксинус	Ж. Лагранж	1772
Sh	гиперболический синус	В. Риккати	1757
Ch	гиперболический косинус
dx, ddx, …	дифференциал	Г. Лейбниц	1675 (в печати 1684)
d 2x, d 3x,…
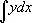	интеграл	Г. Лейбниц	1675 (в печати 1686)
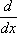	производная	Г. Лейбниц	1675
¦¢x	производная	Ж. Лагранж	1770, 1779
y’
¦¢(x)
Dx	разность	Л. Эйлер	1755
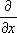	частная производная	А. Лежандр	1786
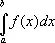	определённый интеграл	Ж. Фурье	1819-22
S	сумма	Л. Эйлер	1755
П	произведение	К. Гаусс	1812
!	факториал	К. Крамп	1808
|x|	модуль	К. Вейерштрасс	1841
lim	предел	У. Гамильтон, многие математики	1853, начало 20 в.
lim
n = ¥
lim
n ® ¥
x	дзета-функция	Б. Риман	1857
Г	гамма-функция	А. Лежандр	1808
В	бета-функция	Ж. Бине	1839
D	дельта (оператор Лапласа)	Р. Мёрфи	1833
Ñ	набла (оператор Гамильтона)	У. Гамильтон	1853
Знаки переменных операций
jx	функция	И. Бернули	1718
f ('x)	Л. Эйлер	1734
Знаки индивидуальных отношений
='	равенство	Р. Рекорд	1557
>'	больше	Т. Гарриот	1631
<'	меньше
º	сравнимость	К. Гаусс	1801
||	параллельность	У. Оутред	1677
^	перпендикулярность	П. Эригон	1634

И. Ньютон в своём методе флюксий и флюент (1666 и следующие гг.) ввёл знаки для последовательных флюксий (производных) величины (в виде

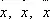
и для бесконечно малого приращения o . Несколько ранее Дж. Валлис (1655) предложил знак бесконечности ¥.

Создателем современной символики дифференциального и интегрального исчислений является Г. Лейбниц. Ему, в частности, принадлежат употребляемые ныне З. м. дифференциалов

dx, d 2 x, d 3 x

и интеграла

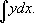
Огромная заслуга в создании символики современной математики принадлежат Л. Эйлеру. Он ввёл (1734) в общее употребление первый знак переменной операции, именно знак функции f ( x ) (от лат. functio). После работ Эйлера знаки для многих индивидуальных функций, например тригонометрических, приобрели стандартный характер. Эйлеру же принадлежат обозначения постоянных е (основание натуральных логарифмов, 1736), p [вероятно, от греческого perijereia (periphereia) — окружность, периферия, 1736], мнимой единицы