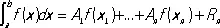 ,
,
где x 1, x 2..., x n— узлы К. ф., А 1 , А 2 , …А n— её коэффициенты и R n— остаточный член. Например,
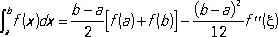 ,
,
где a £ x £ b (формула трапеций). Иногда К. ф. называют также формулами механических, исчисленных квадратур. См. также Котеса формулы , Симпсона формула , Чебышева формула .
Лит.: Крылов В. И., Приближенное вычисление интегралов, 2 изд., М 1967.
Квадри'виум(лат. quadrivium, буквально — пересечение четырех дорог), повышенный курс светского образования в средневековой школе, состоявший из 4 предметов: музыки, арифметики, геометрии и астрономии. Вместе с начальным курсом тривиумом К. составлял так
называемые «семь свободных искусств» .
Квадри'га(лат. quadriga), античная (древнегреческая, римская) колесница на 2-х колёсах, запряжённая четвёркой лошадей, расположенных в 1 ряд: возница управлял ими стоя. Лёгкие К. применялись для конских состязаний, занимавших большое место в Олимпийских и др. общественных играх. Описания этих состязаний есть у Гомера, Вергилия и др. античных авторов. Массивными К. пользовались императоры и полководцы-победители для торжественных процессий. Скульптурные изображения К. с античными божествами или аллегорическими фигурами славы, счастья и т.п. в качестве возниц служили украшением античных строении. Барельефы с изображением К. часто встречаются на античных медалях, камеях и геммах . В России и Западной Европе 18—19 вв. К. украшались фронтоны монументальных здании и триумфальные арки.
Квадриллио'н(франц. quadrillion), число, изображаемое единицей с 15 нулями, т. е. число 10 15. Иногда К. называют число 10 24.
Квадри'руемая о'бласть,область, имеющая определённую площадь , или, что то же — определённую плоскую меру в смысле Жордана (см. Мера множества ). Отличительным свойством К. о. D является возможность заключить её «между» двумя многоугольниками так, чтобы один из них содержался внутри данной К. о., другой, напротив, содержал её внутри, а разность их площадей могла бы быть произвольно малой. В этом случае существует только одно число, заключённое между площадями всех «охватывающих» и «охватываемых» многоугольников; его и называют площадью К. о. D . Свойства квадрируемых областей: если К. о. D содержится в К. о. D 1, то площадь D не превосходит площади D 1; область D , состоящая из двух непересекающихся К. о. D 1 и D 2, квадрируема, и её площадь равна сумме площадей областей D 1и D 2; общая часть двух К. о. D 1и D 2снова является К. о. Для того чтобы область D была квадрируема, необходимо и достаточно, чтобы её граница имела площадь, равную нулю; существуют области, не удовлетворяющие этому условию и, следовательно, неквадрируемые.
Квадрупо'ль(от лат. quadrum — четырёхугольник, квадрат и греч. pólos — полюс), система заряженных частиц, полный электрический заряд и электрический дипольный момент которой равны нулю. К. можно рассматривать как совокупность двух одинаковых диполей с равными по величине и противоположными по направлению дипольными моментами, расположенных на некотором расстоянии друг от друга (см. рис. ). На больших расстояниях R от К. напряженность его электрического поля E убывает обратно пропорционально четвёртой степени R ( E ~ 1/ R 4), а зависимость Е от зарядов и их расположения описывается в общем случае набором из пяти независимых величин, которые, вместе составляют квадрупольный момент системы. Квадрупольный момент определяет также энергию К. во внешнем электрическом поле. В частном случае К., изображенных на рис. , квадрупольный момент по абсолютной величине равен 2 ela , где е — заряд, l — размер диполей, а — расстояние между центрами диполей. К. является мультиполем 2-го порядка.
Лит.: Ландау Л. Д. и Лифшиц Е. М., Теория поля, 5 изд., М., 1967, § 41.
Г. Я. Мякишев.
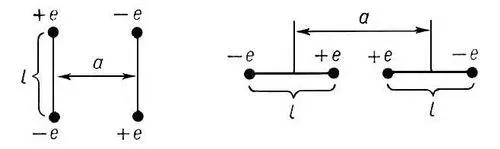
Примеры относительного расположения диполей в квадруполе.
Читать дальше

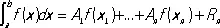 ,
,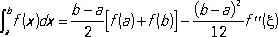 ,
,