Квадра'т(от лат. quadratus — четырёхугольный), 1) равносторонний прямоугольник. К. является правильным многоугольником . 2) К. числа а — произведение а × а = a 2, название связано с тем, что именно таким произведением выражается площадь квадрата, сторона которого равна а .
Квадрати'чная оши'бка,понятие теории вероятностей и математической статистики. См. Квадратичное отклонение .
Квадрати'чная фо'рма,форма 2-й степени от n переменных x 1, x 2 ,..., x n, т. е. многочлен от этих переменных, каждый член которого содержит либо квадрат одного из переменных, либо произведение двух различных переменных. Общий вид К. ф. при n = 2:
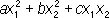 ,
,
при n = 3:
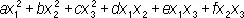 ,
,
где a , b ,..., f — какие-либо числа. Произвольная К. ф. записывается так:
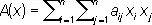 ;
;
причём считают, что a ij = a j i. К. ф. от 2, 3 и 4 переменных непосредственно связаны с теорией линий (на плоскости) и поверхностей (в пространстве) 2-го порядка: в декартовых координатах уравнение линии и поверхности 2-го порядка, отнесённых к центру, имеет вид А ( х ) = 1, т. е. его левая часть является К. ф.; в однородных координатах левая часть любого уравнения линии и поверхности 2-го порядка является К. ф. При замене переменных x 1, x 2,..., x nдр. переменными y 1, y 2,..., y n, являющимися линейными комбинациями старых переменных, К. ф. переходит в другую К. ф. Путём соответствующего выбора новых переменных (невырожденного линейного преобразования) можно привести К. ф. к виду суммы квадратов переменных, умноженных на некоторые числа. При этом ни число квадратов (ранг К. ф.), ни разность между числом положительных и числом отрицательных коэффициентов при квадратах (сигнатура К. ф.) не зависят от способа приведения К. ф. к сумме квадратов (закон инерции). Указанное приведение можно осуществить даже специальными (т. н. ортогональными) преобразованиями. Геометрически в этом случае такое преобразование соответствует приведению линии или поверхности 2-го порядка к главным осям.
При рассмотрении комплексных переменных изучаются К. ф. вида
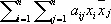
где 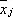 — число, комплексно сопряженное с x j. Если, кроме того, такая К. ф. принимает только действительные значения (это будет, когда (
— число, комплексно сопряженное с x j. Если, кроме того, такая К. ф. принимает только действительные значения (это будет, когда ( 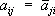 ), то её называют эрмитовой. Для эрмитовых форм справедливы основные факты, относящиеся к действительным К. ф.: возможность приведения к сумме квадратов, инвариантность ранга, закон инерции.
), то её называют эрмитовой. Для эрмитовых форм справедливы основные факты, относящиеся к действительным К. ф.: возможность приведения к сумме квадратов, инвариантность ранга, закон инерции.
Лит.: Мальцев А. И., Основы линейной алгебры, 3 изд., М., 1970.
Квадрати'чное отклоне'ние,квадратичное уклонение, стандартное отклонение величин x 1, x 2,..., x n от а — квадратный корень из выражения
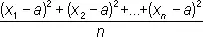 .
.
Наименьшее значение К. о. имеет при а = 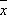 , где
, где 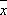 — среднее арифметическое величин x 1, x 2,..., x n:
— среднее арифметическое величин x 1, x 2,..., x n:
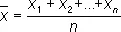 .
.
В этом случае К. о. может служить мерой рассеяния системы величин x 1, x 2,..., x n. Употребляют также более общее понятие взвешенного К. о.
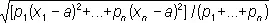 ;
;
числа p 1,..., p nназывают при этом весами, соответствующими величинам x 1,..., x n. Взвешенное К. о. достигает наименьшего значения при а , равном взвешенному среднему:
( p 1 x 1 + ... + p n x n)/( p 1 + ...+ p n).
В теории вероятностей К. о. ох случайной величины Х (от её математического ожидания) называют квадратный корень из дисперсии 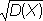 .
.
Читать дальше

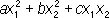 ,
,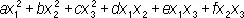 ,
,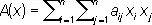 ;
;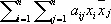
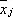 — число, комплексно сопряженное с x j. Если, кроме того, такая К. ф. принимает только действительные значения (это будет, когда (
— число, комплексно сопряженное с x j. Если, кроме того, такая К. ф. принимает только действительные значения (это будет, когда ( 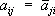 ), то её называют эрмитовой. Для эрмитовых форм справедливы основные факты, относящиеся к действительным К. ф.: возможность приведения к сумме квадратов, инвариантность ранга, закон инерции.
), то её называют эрмитовой. Для эрмитовых форм справедливы основные факты, относящиеся к действительным К. ф.: возможность приведения к сумме квадратов, инвариантность ранга, закон инерции.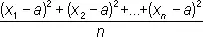 .
.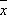 , где
, где 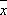 — среднее арифметическое величин x 1, x 2,..., x n:
— среднее арифметическое величин x 1, x 2,..., x n: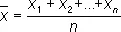 .
.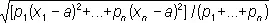 ;
;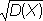 .
.