Э. Г. Позняк.
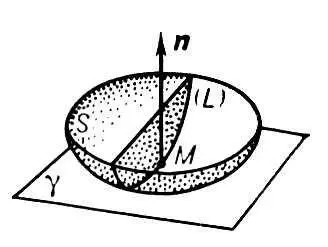
Рис. 1 к ст. Поверхностей теория.
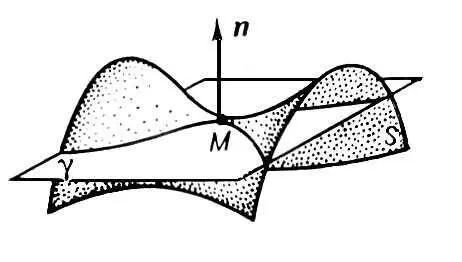
Рис. 2 к ст. Поверхностей теория.
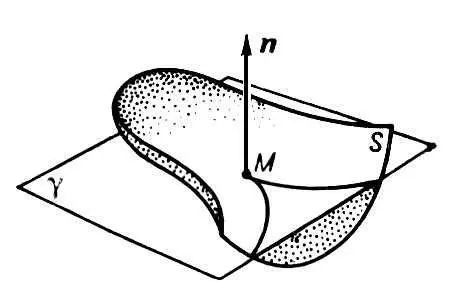
Рис. 3 к ст. Поверхностей теория.
Пове'рхности враще'ния, поверхности, образуемые вращением плоской кривой вокруг прямой (оси П. в.), расположенной в плоскости этой линии. Примером П. в. может служить сфера (которую можно рассматривать как поверхность, образованную вращением полуокружности вокруг её диаметра). Линии пересечения П. в. с плоскостями, проходящими через её ось, называется меридианами; линии пересечения П. в. с плоскостями, перпендикулярными оси, — параллелями. Если по оси П. в. направить ось Oz прямоугольной системы координат Oxyz, то параметрическое уравнения П. в. можно записать следующим образом:
x = f ( u ) cosu, y = f ( u ) sinu, z = u.
[здесь f ( u ) — функция, определяющая форму меридиана, а u — угол поворота плоскости меридиана].
Поверхности второго порядка
Пове'рхности второ'го поря'дка, поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени:
a 11 x 2+ a 22 y 2+ a 33 z 2+ 2 a 12 xy + 2 a 23 yz + 2 a 13 xz + 2 a 14 x + 2 a 24 y + 2 a 34 z + a 44= 0 (*)
Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из 17 приведённых ниже канонических видов, каждому из которых соответствует определённый класс П. в. п. Среди них выделяют пять основных типов поверхностей. Именно,
1) эллипсоиды
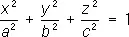 — эллипсоиды,
— эллипсоиды,
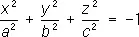 — мнимые эллипсоиды;
— мнимые эллипсоиды;
2) гиперболоиды:
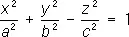 — однополостные гиперболоиды,
— однополостные гиперболоиды,
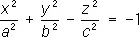 — двуполостные гиперболоиды;
— двуполостные гиперболоиды;
3) параболоиды ( p > 0, q > 0):
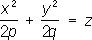 — эллиптические параболоиды,
— эллиптические параболоиды,
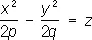 — гиперболические параболоиды;
— гиперболические параболоиды;
4) конусы второго порядка:
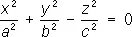 — конусы,
— конусы,
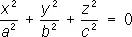 — мнимые конусы;
— мнимые конусы;
5) цилиндры второго порядка:
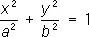 — эллиптические цилиндры,
— эллиптические цилиндры,
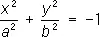 — мнимые эллиптические цилиндры,
— мнимые эллиптические цилиндры,
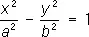 — гиперболические цилиндры,
— гиперболические цилиндры,
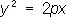 — параболические цилиндры.
— параболические цилиндры.
Перечисленные П. в. п. относятся к т. н. нераспадающимся П. в. п.; распадающиеся П. в. п.:
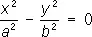 — пары пересекающихся плоскостей,
— пары пересекающихся плоскостей,
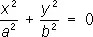 —пары мнимых пересекающихся плоскостей,
—пары мнимых пересекающихся плоскостей,
х 2 = а 2 — пары параллельных плоскостей,
х 2 = —а 2 — пары мнимых параллельных плоскостей,
х 2 = 0 — пары совпадающих плоскостей.
При исследовании общего уравнения П. в. п. важное значение имеют т. н. основные инварианты — выражения, составленные из коэффициентов уравнения (*) и не меняющиеся при параллельном переносе и повороте системы координат. Например, если
Читать дальше




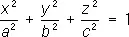 — эллипсоиды,
— эллипсоиды,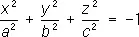 — мнимые эллипсоиды;
— мнимые эллипсоиды;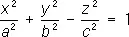 — однополостные гиперболоиды,
— однополостные гиперболоиды,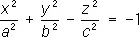 — двуполостные гиперболоиды;
— двуполостные гиперболоиды;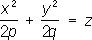 — эллиптические параболоиды,
— эллиптические параболоиды,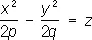 — гиперболические параболоиды;
— гиперболические параболоиды;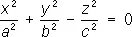 — конусы,
— конусы,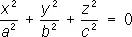 — мнимые конусы;
— мнимые конусы;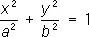 — эллиптические цилиндры,
— эллиптические цилиндры,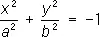 — мнимые эллиптические цилиндры,
— мнимые эллиптические цилиндры,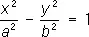 — гиперболические цилиндры,
— гиперболические цилиндры,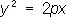 — параболические цилиндры.
— параболические цилиндры.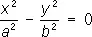 — пары пересекающихся плоскостей,
— пары пересекающихся плоскостей,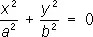 —пары мнимых пересекающихся плоскостей,
—пары мнимых пересекающихся плоскостей,