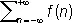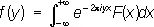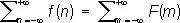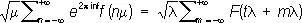Решение краевых задач для П. у. сводится подстановкой 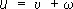 к решению краевых задач для уравнения Лапласа Dw = 0.
к решению краевых задач для уравнения Лапласа Dw = 0.
П. у. впервые (1812) было изучено С. Д. Пуассоном.
Пуассона формула суммирования
Пуассо'на фо'рмула сумми'рования,формула для вычисления суммы ряда вида
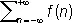
Если
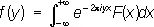
— Фурье преобразование (несколько иначе, чем обычно, нормированное) функции F ( x ), то
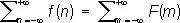
( m и n — целые). Это и есть П. ф. с.; она может быть записана в более общем виде: если l > 0, m > 0, lm = 1 и 0 £ t < 1 , то
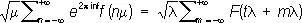
Для справедливости этой формулы достаточно, чтобы в каждом конечном интервале F ( x ) имела ограниченную вариацию, и для х ® + ¥ и х ® — ¥ выполнялось одно из условий: 1) F ( x ) — монотонна и абсолютно интегрируема; 2) F ( x ) — интегрируема и обладает абсолютно интегрируемой производной. П. ф. с. позволяет в ряде случаев заменить вычисление суммы ряда вычислением суммы др. ряда, сходящегося быстрее первоначального.
Пуассо'новский пото'к,то же, что пуассоновский процесс. Этот термин используют, как правило, в массового обслуживания теории.
Пуассо'новский проце'сс,случайный процесс, описывающий моменты наступления 0 < t 1<...< t n<...<... каких-либо случайных событий, в котором число событий, происходящих в течение любого фиксированного интервала времени, имеет Пуассона распределение и независимы числа событий, происходящих в непересекающиеся промежутки времени.
Пусть m( s , t ) — число событий, моменты наступления которых t iудовлетворяют неравенствам 0 £ s < t i£ t , и пусть l( s, t ) — математическое ожидание m( s , t ) . Тогда и П. п. при любых 0 £ s 1 < t 1 £ s 2 < t 2£... £ s r< t rслучайные величины m( s 1, t 1), m( s 2, t 2),... m( s r, t r) независимы и вероятность того, что m(s, t ) = n, равна
e - l (s, t)[l( s, t )] n/ n !.
В однородном П. п. l( s, t ) = a ( t — s ) , где а — среднее число событий в единицу времени, расстояния t n — t n-1 между соседними моментами t nнезависимы и имеют показательное распределение с плотностью ae -at, t ³ 0.
Если имеется много независимых процессов, описывающих моменты возникновения некоторых случайных редких событий, то суммарный процесс при определённых условиях в пределе даёт П. п.
П. п. представляет собой удобную математическую модель, которая часто используется в различных приложениях теории вероятностей. В частности, с помощью П. п. описывается поток требований (например, вызовов, поступающих на телефонную станцию, выездов медицинских машин скорой помощи при транспортных происшествиях в большом городе) в массового обслуживания теории.
Обобщением П. п. является пуассоновское случайное распределение точек на плоскости или в пространстве, при котором число точек в любой фиксированной области имеет распределение Пуассона (со средним, пропорциональным площади или объёму области) и числа точек в непересекающихся областях независимы. Это распределение часто используется при расчётах в астрономии, физике, экологии, технике и т.д.
Лит.: Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., т. 1—2, М., 1967.
Б. А. Севастьянов.
Пуату'(Poitou), историческая область на З. Франции, у побережья Атлантического океана. На территории П. — департаменты Вандея, Вьенна, Дё-Севр. П. (без Вандеи) вместе с историческими областями Они, Сентонж и Ангумуа (территория современных департаментов Шаранта и Приморская Шаранта) составляют плановый экономический район Пуату — Шаранта. Площадь П. 20,1 тыс. км 2 . Население 1,1 млн. чел. (1973). Главный город — Пуатье. Территория области — большей частью всхолмлённая равнина; типичен бокаж. Главная отрасль экономики — сельское хозяйство, особенно животноводство (крупный рогатый скот, свиньи) и птицеводство. Основные с.-х. культуры: пшеница, ячмень, кормовые; овощеводство. Промышленность занята главным образом переработкой с.-х. сырья. В гг. Шательро и Пуатье — машиностроение. В районе Мортань — добыча урановой руды (обогащение — на заводе в Экарпьер).
Читать дальше

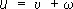 к решению краевых задач для уравнения Лапласа Dw = 0.
к решению краевых задач для уравнения Лапласа Dw = 0.