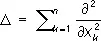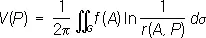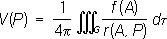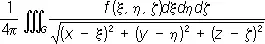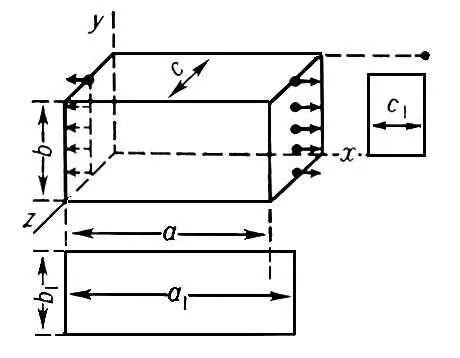
Рис. к ст. Пуассона коэффициент.
Пуассо'на распределе'ние,одно из важнейших распределений вероятностей случайных величин, принимающих целочисленные значения. Подчинённая П. р. случайная величина Х принимает лишь неотрицательные значения, причём Х = kc вероятностью
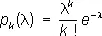 , k = 0, 1, 2,...
, k = 0, 1, 2,...
(l — положительный параметр). Своё название «П. р.» получило по имени С. Д. Пуассона (1837). Математическое ожидание и дисперсия случайной величины, имеющей П. р. с параметром l, равны l. Если независимые случайные величины X 1 и X 2 имеют П. р. с параметрами l 1и l 2 , то их сумма X 1 + X 2 имеет П. р. с параметрами l 1+ l 2.
В теоретико-вероятностных моделях П. р. используется как аппроксимирующее и как точное распределение. Например, если при n независимых испытаниях события A 1,..., A n осуществляются с одной и той же малой вероятностью р, то вероятность одновременного осуществления каких-либо k событий (из общего числа n ) приближённо выражается функцией p k ( np ) (математическое содержание этого утверждения при больших значениях n и 1/ р формулируются Пуассона теоремой ). В частности, такая модель хорошо описывает процесс радиоактивного распада и многие др. физические явления.
Как точное П. р. появляется в теории случайных процессов. Например, при расчёте нагрузки линий связи обычно предполагают, что количества вызовов, поступивших за непересекающиеся интервалы времени, суть независимые случайные величины, подчиняющиеся П. р. с параметрами, значения которых пропорциональны длинам соответствующих интервалов времени (см. Пуассоновский процесс ).
В качестве оценки неизвестного параметра l по n наблюдённым значениям независимых случайных величин X 1,..., X nиспользуется их арифметическое среднее X = ( X 1+ ... + X n)/ n, поскольку эта оценка лишена систсматической ошибки и её квадратичное отклонение минимально (см. Статистические оценки ).
Лит.: Гнеденко Б. В., Курс теории вероятностей, 5 изд., М. — Л., 1969; Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967.
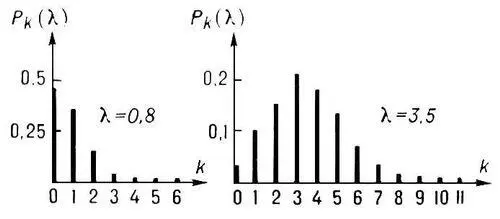
Рис. к ст. Пуассона распределение.
Пуассо'на теоре'ма,1) теорема теории вероятностей, описывающая поведение частоты появления некоторого события в последовательности независимых испытаний — частный случай закона больших чисел (точную формулировку см. в ст. Больших чисел закон ). 2) Одна из предельных теорем теории вероятностей. П. т. позволяет приближённо оценивать вероятность данного числа появлений маловероятного события при большом числе независимых испытаний (см. Пуассона распределение ).
Обе теоремы установлены С. Д. Пуассоном в 1837.
Пуассо'на уравне'ние,уравнение с частными производными вида D u = f, где D —оператор Лапласа:
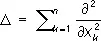
При n = 3 этому уравнению удовлетворяет потенциалu ( х, у, z ) объёмных масс, распределённых с плотностью f ( x, у, z )/4p (в областях, где f = 0 потенциал u удовлетворяет уравнению Лапласа), а также потенциал объёмно распределённых электрических зарядов. При этом плотность распределения f должна удовлетворять известным требованиям гладкости (например, условию непрерывности частных производных). Если функция f отлична от нуля лишь в конечной области G, ограничена и имеет непрерывные частные производные первого порядка, то при n = 2 частное решение П. у. имеет вид:
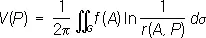
а при n = 3:
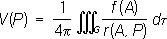
где r ( А , Р ) — расстояние между переменной точкой интегрирования А и некоторой точкой Р . В более подробной записи
V ( х, у, z ) = 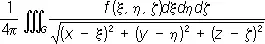
Читать дальше


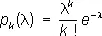 , k = 0, 1, 2,...
, k = 0, 1, 2,...