Лит. см. при ст. Сферическая геометрия.
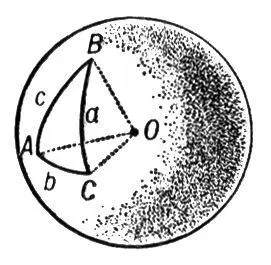
Рис. к ст. Сферическая тригонометрия.
Сфери'ческие координа'тыточки М, три числа r , q , j , которые определяются следующим образом. Через фиксированную точку О ( рис. ) проводятся три взаимно оси Ox, Оу, Oz. Число r равно расстоянию от точки О до точки М, q представляет собой угол между вектором 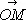 и положительным направлением оси Oz, j — угол, на который надо повернуть против часовой стрелки положительную полуось Ox до совпадения с вектором
и положительным направлением оси Oz, j — угол, на который надо повернуть против часовой стрелки положительную полуось Ox до совпадения с вектором 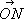 ( N — проекция точки М на плоскость хОу ) . С. к. точки М зависят, таким образом, от выбора точки О и трёх осей Ox, Оу, Oz. Связь С. к. с прямоугольными декартовыми координатами устанавливается следующими формулами:
( N — проекция точки М на плоскость хОу ) . С. к. точки М зависят, таким образом, от выбора точки О и трёх осей Ox, Оу, Oz. Связь С. к. с прямоугольными декартовыми координатами устанавливается следующими формулами:
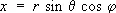 ,
, 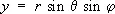 ,
, 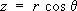 .
.
С. к. имеют большое применение в математике и её приложениях к физике и технике.
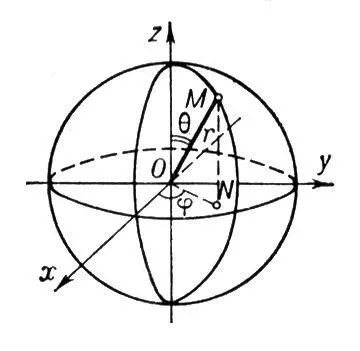
Рис. к ст. Сферические координаты.
Сфери'ческие фу'нкции,специальные функции, применяемые для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями, и для решения физических задач, обладающих сферической симметрией. С. ф. являются решениями дифференциального уравнения
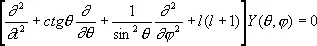 ,
,
получающегося при разделении переменных в Лапласа уравнении в сферических координатах r, q, j . Общий вид решения:
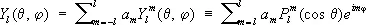 ,
,
где a m— постоянные, 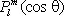 — присоединённые функции Лежандра степени l и порядка m, определяемые равенством:
— присоединённые функции Лежандра степени l и порядка m, определяемые равенством:
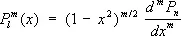 ,
,
где Р п— Лежандра многочлены.
С. ф. можно рассматривать как функции на поверхности единичной сферы. Функции
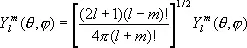
образуют полную ортонормированную систему на сфере, играющую ту же роль в разложении функций на сфере, что тригонометрическая система функций { e im j } на окружности. Функции на сфере, не зависящие от координаты j, разлагаются по зональным С. ф.:
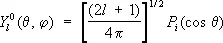
С. ф. степени l
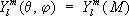
при вращении сферы линейно преобразуется по формуле:
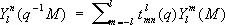 (1)
(1)
( q –1 M — точка, в которую переходит точка М сферы при вращении q –1) . Коэффициенты 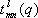 являются матричными элементами неприводимого унитарного представления веса l группы вращения сферы. Их называют также обобщёнными С. ф. Обобщённые С. ф. применяются при разложении векторных и тензорных полей на единичной сфере, решении некоторых задач теории упругости и т. д.
являются матричными элементами неприводимого унитарного представления веса l группы вращения сферы. Их называют также обобщёнными С. ф. Обобщённые С. ф. применяются при разложении векторных и тензорных полей на единичной сфере, решении некоторых задач теории упругости и т. д.
С формулой (1) связана теорема сложения для зональных С. ф.:
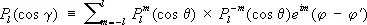 ,
,
где cos g = cos q cos q‘ + sinq sinq' cos (j —j’), g — сферическое расстояние точки (q, j) от точки (q', j’).
Характерным примером многочисленных приложений С. ф. к вопросам математической физики и механики является применение их в теории потенциала. Пусть 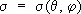 — поверхностная плотность распределения массы по сфере радиуса R с центром в начале координат; если а можно разложить в ряд С. ф.
— поверхностная плотность распределения массы по сфере радиуса R с центром в начале координат; если а можно разложить в ряд С. ф. 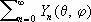 , сходящийся равномерно на поверхности сферы, то потенциал, соответствующий этому распределению масс, в каждой точке ( r , q, j ), внешней относительно данной сферы, равен
, сходящийся равномерно на поверхности сферы, то потенциал, соответствующий этому распределению масс, в каждой точке ( r , q, j ), внешней относительно данной сферы, равен
Читать дальше


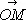 и положительным направлением оси Oz, j — угол, на который надо повернуть против часовой стрелки положительную полуось Ox до совпадения с вектором
и положительным направлением оси Oz, j — угол, на который надо повернуть против часовой стрелки положительную полуось Ox до совпадения с вектором 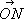 ( N — проекция точки М на плоскость хОу ) . С. к. точки М зависят, таким образом, от выбора точки О и трёх осей Ox, Оу, Oz. Связь С. к. с прямоугольными декартовыми координатами устанавливается следующими формулами:
( N — проекция точки М на плоскость хОу ) . С. к. точки М зависят, таким образом, от выбора точки О и трёх осей Ox, Оу, Oz. Связь С. к. с прямоугольными декартовыми координатами устанавливается следующими формулами: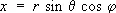 ,
, 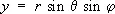 ,
, 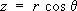 .
.
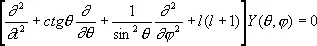 ,
,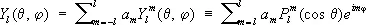 ,
,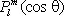 — присоединённые функции Лежандра степени l и порядка m, определяемые равенством:
— присоединённые функции Лежандра степени l и порядка m, определяемые равенством: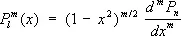 ,
,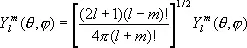
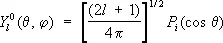
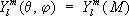
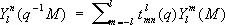 (1)
(1)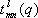 являются матричными элементами неприводимого унитарного представления веса l группы вращения сферы. Их называют также обобщёнными С. ф. Обобщённые С. ф. применяются при разложении векторных и тензорных полей на единичной сфере, решении некоторых задач теории упругости и т. д.
являются матричными элементами неприводимого унитарного представления веса l группы вращения сферы. Их называют также обобщёнными С. ф. Обобщённые С. ф. применяются при разложении векторных и тензорных полей на единичной сфере, решении некоторых задач теории упругости и т. д.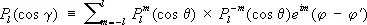 ,
,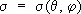 — поверхностная плотность распределения массы по сфере радиуса R с центром в начале координат; если а можно разложить в ряд С. ф.
— поверхностная плотность распределения массы по сфере радиуса R с центром в начале координат; если а можно разложить в ряд С. ф. 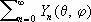 , сходящийся равномерно на поверхности сферы, то потенциал, соответствующий этому распределению масс, в каждой точке ( r , q, j ), внешней относительно данной сферы, равен
, сходящийся равномерно на поверхности сферы, то потенциал, соответствующий этому распределению масс, в каждой точке ( r , q, j ), внешней относительно данной сферы, равен