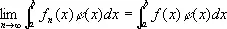
для любой функции j(x) с интегрируемым квадратом (например, последовательность функций sinx, sin2x,..., sinnx, ... слабо сходится к нулю на отрезке [—p, p], так как для любой функции j(х) с интегрируемым квадратом коэффициенты 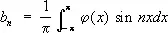 ряда Фурье стремятся к нулю).
ряда Фурье стремятся к нулю).
Указанные выше и многие другие понятия С. последовательности функций систематически изучаются в функциональном анализе, где рассматриваются различные линейные пространства с заданной нормой (расстоянием до нуля) — так называемые банаховы пространства. В таких пространствах можно ввести понятия С. функционалов, операторов и т. д., определяя для них соответствующим образом норму. Наряду со С. по норме (так называемой сильной С.), в банаховых пространствах рассматривается слабая С., определяемая условием 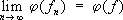 для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы
для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы 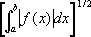 . В современной математике рассматривается также С. по частично упорядоченным множествам (см. Упорядоченные и частично упорядоченные множества ) . В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.
. В современной математике рассматривается также С. по частично упорядоченным множествам (см. Упорядоченные и частично упорядоченные множества ) . В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.
Ещё математики древности (Евклид, Архимед) по существу употребляли бесконечные ряды для нахождения площадей и объёмов. Доказательством С. рядов им служили вполне строгие рассуждения по схеме исчерпывания метода. Термин «С.» в применении к рядам был введён в 1668 Дж. Грегори при исследовании некоторых способов вычисления площади круга и гиперболического сектора. Математики 17 в. обычно имели ясное представление о С. употребляемых ими рядов, хотя и не проводили строгих с современной точки зрения доказательств С. В 18 в. широко распространилось употребление в анализе заведомо расходящихся рядов (в частности, их широко применял Л. Эйлер ) . Это, с одной стороны, привело впоследствии ко многим недоразумениям и ошибкам, устранённым лишь с развитием отчётливой теории С., а с другой — предвосхитило современную теорию суммирования расходящихся рядов. Строгие методы исследования С. рядов были разработаны в 19 в. (О. Коши, Н. Абель, К . Вейерштрасс, Б . Больцано и др.). Понятие равномерной С. было введено Дж. Стоксом. Дальнейшие расширения понятия С. были связаны с развитием теории функций, функционального анализа и топологии.
Лит.: Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., т. 1—2, М., 1971—73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1—2, М., 1970; Никольский С. М., Курс математического анализа, т. 1—2, М., 1973.
Схо'дница,посёлок городского типа в Львовской области УССР. Подчинён Бориславскому горсовету. Расположен в 9 км от ж.-д. станции Борислав. Нефтепромысел, лесозавод и др. предприятия. Пансионаты: «Карпаты», «Гуцулка».
Схо'дня,город (с 1961) в Химкинском районе Московской области РСФСР, на р. Сходня (приток р. Москвы). Ж.-д. станция в 30 км к С.-З. от Москвы. 19 тыс. жителей (1974). Стекольный завод, мебельно-сборочный комбинат, галантерейная и трикотажная фабрики. Пушно-меховой техникум. Турбаза.
Схо'дство(философский), соответствие отображения, образа своему оригиналу. Понятие С. используется при моделировании. Оно включает три основные отношения: соответствие качественных характеристик отображения особенностям оригинала (например, ощущение зелёного цвета листьев растения соответствует определённой длине электромагнитных волн, излучаемых поверхностью листьев); соответствие структур отображения структурам оригинала (например, структура географической карты соответствует геометрическим структурам местности), причём разные виды соответствия структур могут описываться с помощью различных математических отображений — изоморфизма, гомоморфизма и др.; соответствие количественных характеристик отображения и оригинала (например, количественные значения состояний термостата соответствует измеряемой температуре тела).
Читать дальше

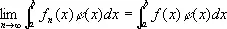
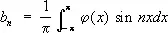 ряда Фурье стремятся к нулю).
ряда Фурье стремятся к нулю).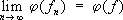 для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы
для всех линейных функционалов; введённая выше слабая С. функций соответствует рассмотрению нормы 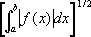 . В современной математике рассматривается также С. по частично упорядоченным множествам (см. Упорядоченные и частично упорядоченные множества ) . В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.
. В современной математике рассматривается также С. по частично упорядоченным множествам (см. Упорядоченные и частично упорядоченные множества ) . В теории вероятностей для последовательности случайных величин употребляются понятия С. с вероятностью 1 и С. по вероятности.