Большую роль понятие С. играет при решении всевозможных уравнений (алгебраических, дифференциальных, интегральных), в частности при нахождении их численных приближённых решений. Например, с помощью последовательных приближений метода можно получить последовательность функций, сходящихся к соответствующему решению данного обыкновенного дифференциального уравнения, и тем самым одновременно доказать существование при определённых условиях решения и дать метод, позволяющий вычислить это решение с нужной точностью. Как для обыкновенных дифференциальных уравнений, так и уравнений с частными производными существует хорошо разработанная теория различных сходящихся конечноразностных методов их численного решения (см. Сеток метод ) . Для практического нахождения приближённых решений уравнений широко используются ЭВМ.
Если изображать члены a n последовательности { a n } на числовой прямой, то С. этой последовательности к а означает, что расстояние между точками a n и а становится и остаётся сколь угодно малым с возрастанием n. В этой формулировке понятие С. обобщается на последовательности точек плоскости, пространства и более общих объектов, для которых может быть определено понятие расстояния, обладающее обычными свойствами расстояния между точками пространства (например, на последовательности векторов, матриц, функций, геометрических фигур и т. д., см. Метрическое пространство ) . Если последовательность { a n } сходится к а, то вне любой окрестности точки а лежит лишь конечное число членов последовательности. В этой формулировке понятие С. допускает обобщение на совокупности величин ещё более общей природы, в которых тем или иным образом введено понятие окрестности (см. Топологическое пространство ) .
В математическом анализе используются различные виды С. последовательности функций { f n ( x )} к функции f ( x ) (на некотором множестве М). Если 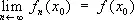 для каждой точки X 0 (из М ) , то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см. Мера множества ) , то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций f n ( x ) к f ( x ) в каждой точке не следует, вообще говоря, С. интегралов от функций f n ( x ) к интегралу от f ( x ) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность { f n ( x )} называется равномерно сходящейся к f ( x ) на множестве М, если
для каждой точки X 0 (из М ) , то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см. Мера множества ) , то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций f n ( x ) к f ( x ) в каждой точке не следует, вообще говоря, С. интегралов от функций f n ( x ) к интегралу от f ( x ) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность { f n ( x )} называется равномерно сходящейся к f ( x ) на множестве М, если
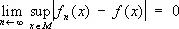
Этот вид С. соответствует определению расстояния между функциями f ( x ) и ( 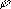 ( х ) по формуле
( х ) по формуле
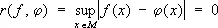
Д. Ф. Егоров доказал, что если последовательность измеримых функций сходится почти всюду на множестве М, то из М можно так удалить часть сколь угодно малой меры, чтобы на оставшейся части имела место равномерная С.
В теории интегральных уравнений, ортогональных рядов и т. д. широко применяется понятие средней квадратической С.: последовательность { f n ( x )} сходится на отрезке [ a, b ] в среднем квадратическом к f ( x ) , если
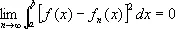 .
.
Более общо, последовательность { f n ( x )} сходится в среднем с показателем р к f ( x ) , если
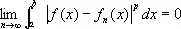 .
.
Эта С. соответствует заданию расстояния между функциями по формуле
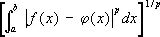 .
.
Из равномерной С. на конечном отрезке вытекает С. в среднем с любым показателем р. Последовательность частичных сумм разложения функции j(х) с интегрируемым квадратом по нормированной ортогональной системе функций может расходиться в каждой точке, но такая последовательность всегда сходится к j(х) в среднем квадратическом. Рассматриваются также другие виды С. Например, С. по мере: для любого e > 0 мера множества тех точек, для которых 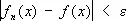 , стремится к нулю с возрастанием n', слабая С.:
, стремится к нулю с возрастанием n', слабая С.:
Читать дальше

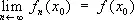 для каждой точки X 0 (из М ) , то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см. Мера множества ) , то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций f n ( x ) к f ( x ) в каждой точке не следует, вообще говоря, С. интегралов от функций f n ( x ) к интегралу от f ( x ) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность { f n ( x )} называется равномерно сходящейся к f ( x ) на множестве М, если
для каждой точки X 0 (из М ) , то говорят о С. в каждой точке [если это равенство не имеет места лишь для точек, образующих множество меры нуль (см. Мера множества ) , то говорят о С. почти всюду]. Несмотря на свою естественность, понятие С. в каждой точке обладает многими нежелательными особенностями [например, последовательность непрерывных функций может сходиться в каждой точке к разрывной функции; из С. функций f n ( x ) к f ( x ) в каждой точке не следует, вообще говоря, С. интегралов от функций f n ( x ) к интегралу от f ( x ) и т. д.]. В связи с этим было введено понятие равномерной С., свободное от этих недостатков: последовательность { f n ( x )} называется равномерно сходящейся к f ( x ) на множестве М, если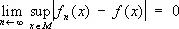
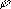 ( х ) по формуле
( х ) по формуле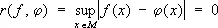
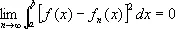 .
.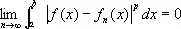 .
.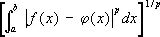 .
.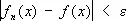 , стремится к нулю с возрастанием n', слабая С.:
, стремится к нулю с возрастанием n', слабая С.: