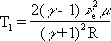e 1— e 0= ( p 1+ p 0 ) ( V 0— V 1 ),
w 1— w 0= ( p 1— p 0 ) ( V 0+ V 1 ), (2)
где V = 1/r — удельный объём, w = e + p / r — удельная энтальпия. Если известны термодинамические свойства вещества, то есть функции e( р ,r) или w( p, r) , то ударная адиабата даёт зависимость конечного давления p 1от конечного объёма V 1при ударном сжатии вещества из данного начального состояния p 0, V 0, то есть зависимость p 1= H ( V 1 , p 0 , V 0).
При переходе через У. в. энтропия вещества S меняется, причём скачок энтропии S 1 — S 0для данного вещества определяется только законами сохранения (1), которые допускают существование двух режимов: скачка сжатия (r 1> r 0, p 1> p 0) и скачка разрежения (r 1< r 0, p 1< p 0). Однако в соответствии со вторым началом термодинамики реально осуществляется только тот режим, при котором энтропия возрастает. В обычных веществах энтропия возрастает только в У. в. сжатия, поэтому У. в. разрежения не реализуется (теорема Цемплена).
У. в. распространяется по невозмущённому веществу со сверхзвуковой скоростью u 0 > a 0(где a 0— скорость звука в невозмущённом веществе) тем большей, чем больше интенсивность У. в., то есть чем больше ( p 1— p 0) / p 0. При стремлении интенсивности У. в. к 0 скорость её распространения стремится к a 0. Скорость У. в. относительно сжатого газа, находящегося за ней, является дозвуковой: u 1 < a 1( a 1— скорость звука в сжатом газе за У. в.).
У. в. в идеальном газе с постоянной теплоёмкостью. Это наиболее простой случай распространения У. в., так как уравнение состояния имеет предельно простой вид: e = р /r(g—1), р = R r T /m, где g = c p /c v — отношение теплоёмкостей при постоянных давлении и объёме (так называемый показатель адиабаты), R — универсальная газовая постоянная, m — молекулярный вес. уравнение ударной адиабаты можно получить в явном виде:
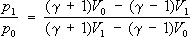 . (3)
. (3)
Ударная адиабата, или адиабата Гюгоньо Н, отличается от обычной адиабаты Р (адиабаты Пуассона), для которой p 1 /p 0 = ( V 0 /V 1) g( рис. 2 ). При ударном сжатии вещества для данного изменения V необходимо большее изменение р, чем при адиабатическом сжатии. Это является следствием необратимости нагревания при ударном сжатии, связанного, в свою очередь, с переходом в тепло кинетической энергии потока, набегающего на фронт У. в. В силу соотношения
u 0 2= V 0 2( р 1- р 0) / ( V 0— V 1 ) , следующего из уравнений (1), скорость У. в. определяется наклоном прямой, соединяющей точки начального и конечного состояний ( рис. 2 ).
Параметры газа в У. в. можно представить в зависимости от Маха числаМ = u в/а 0
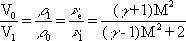 ,
,
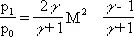 , (4)
, (4)
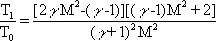 .
.
В пределе для сильных У. в. при М ® ¥; p 1 /p 0® ¥ получается:
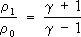 ,
, 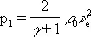 ,
,
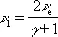 ,
, 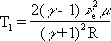
Таким образом, сколь угодно сильная У. в. не может сжать газ более чем в (g + 1)/(g — 1) раз. Например, для одноатомного газа g = и предельное сжатие равно 4, а для двухатомного (воздух) — g = и предельное сжатие равно 6. Предельное сжатие тем выше, чем больше теплоёмкость газа (меньше g) .
Вязкий скачок уплотнения. Необратимость ударного сжатия свидетельствует о наличии диссипации механической энергии во фронте У. в. Диссипативные процессы можно учесть, приняв во внимание вязкость и теплопроводность газа. При этом оказывается, что сам скачок энтропии в У. в. не зависит ни от механизма диссипации, ни от вязкости и теплопроводности газа. Последние определяют лишь внутреннюю структуру фронта волны и его толщину. В У. в. не слишком большой интенсивности все величины — u , р, r и Т монотонно изменяются от своих начальных до конечных значений ( рис. 3 ). Энтропия же S меняется не монотонно и внутри У. в. достигает максимума в точке перегиба скорости, то есть в центре волны. Возникновение максимума S в волне связано с существованием теплопроводности. Вязкость приводит только к возрастанию энтропии, так как благодаря ей происходит рассеяние импульса направленного газового потока, набегающего на У. в., и превращение кинетической энергии направленного движения в энергию хаотического движения, то есть в тепло. Благодаря же теплопроводности тепло необратимым образом перекачивается из более нагретых слоев газа в менее нагретые.
Читать дальше

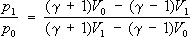 . (3)
. (3)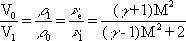 ,
,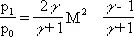 , (4)
, (4)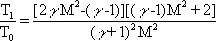 .
.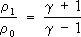 ,
, 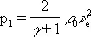 ,
,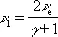 ,
,