БСЭ БСЭ - Большая Советская Энциклопедия (УД)

Соч.: Œuvres, v. 1—10, P., 1754.

Лит.: История французской литературы, т. 1, М.—Л., 1946, с. 604—605; Dost G., Houdar de la Motte als Tragiker und drama-tischer Theoretiker, Weida, 1909.

В. С. Лозовецкий.

Уда'ртвёрдых тел, совокупность явлений, возникающих при столкновении движущихся твёрдых тел, а также при некоторых видах взаимодействия твёрдого тела с жидкостью или газом (У. струи о тело, У. тела о поверхность жидкости, гидравлический удар, действие взрыва или ударной волны на твёрдое тело и др.). Промежуток времени, в течение которого длится У., обычно очень мал (на практике от нескольких десятитысячных до миллионных долей сек ) , а развивающиеся на площадках контакта соударяющихся тел силы (называются ударными или мгновенными) очень велики. Изменяются они за время У. в широких пределах и достигают значений, при которых средние величины давления (напряжений) на площадках контакта имеют порядок 10 4и даже 10 5 кгс/см 2 (1 кгс/см 2= 10 2 н/м 2 ) . Действие ударных сил приводит к значительному изменению за время У. скоростей точек тела. Следствиями У. могут быть также остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств их материалов и др., а при скоростях соударения, превышающих критические, — разрушение тел в месте У. Порядок критических скоростей для металлов » 15 м/сек (медь) — 150 м/сек и более (высококачественные стали).

Изменение скоростей точек тела за время У. определяется методами общей теории У., где в качестве меры механического взаимодействия тел при У. вместо самой ударной силы Р вводится её импульс за время У. t (так называемый ударный импульс S ) . Одновременно, ввиду малости m , импульсами всех неударных сил, таких, например, как сила тяжести, а также перемещениями точек тела за время У. пренебрегают. Основные уравнения общей теории У. вытекают из теорем об изменении количества движения и кинетического момента системы при У. С помощью этих теорем, зная приложенный ударный импульс и скорости в начале У., определяют скорости в конце У., а если тело является несвободным, то и импульсивные реакции связей.

В случае соударения двух тел процесс соударения можно разделить на 2 фазы. 1-я фаза начинается с момента соприкосновения точек А и В тел (см. рис. ), имеющих в этот момент скорость сближения ν An— ν Bn, где ν Аn и ν Bn— проекции скоростей ν Aи ν B на общую нормаль n к поверхностям тел в точках А и В, называется линией удара. К концу 1-й фазы сближение тел прекращается, а часть их кинетической энергии переходит в потенциальную энергию деформации. Во 2-й фазе происходит обратный переход потенциальной энергии упругой деформации в кинетическую энергию тел; при этом тела начинают расходиться и к концу 2-й фазы точки А и В будут иметь скорость расхождения V An— V Bn. Для совершенно упругих тел механическая энергия к концу У. восстановилась бы полностью и было бы | V An—V Bn | = | ν An—ν Bn | , наоборот, У. совершенно неупругих тел закончился бы на 1-й фазе ( V An—V Bn = 0). При У. реальных тел механическая энергия к концу У. восстанавливается лишь частично вследствие потерь на сообщение остаточных деформаций, нагревание тел и др. | V An—V Bn |< | ν An—ν Bn | . Для учёта этих потерь вводится так называемый коэффициент восстановления k, который считается зависящим только от физических свойств материалов тел:

.

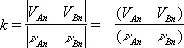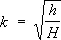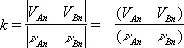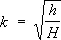В случае У. по неподвижному телу V Bn = ν Bn = 0 и k = – V An / ν An. Значение k определяется экспериментально, например измерением высоты h, на которую отскакивает шарик, свободно падающий на горизонтальную плиту с высоты Н; в этом случае . По данным опытов, при соударении тел из дерева k = 0,5, из стали — 0,55, из слоновой кости — 0,89, из стекла — 0,94. В предельных случаях при совершенно упругом У. k = 1, а при совершенно неупругом k = 0. Зная скорости до У. и коэффициент k, можно найти скорости после У. и действующий в точках соударения ударный импульс S . Ecли центры масс тел C 1и C 2лежат на линии У., то У. называется центральным (У. шаров); в противном случае — нецентральным. Если скорости ν 1 и ν 2 центров масс в начале У. направлены параллельно линии У., то У. называется прямым; в противном случае — косым. При прямом центральном У, двух гладких тел (шаров) 1 и 2