Ким Хо - О чем говорят цифры. Как понимать и использовать данные

Была обнаружена также взаимосвязь между рядом четных чисел и числом π. Более того, π появляется в уравнении «знаменитая пятерка» [79], выведенном великим швейцарским математиком XVIII века Леонардом Эйлером. В 1988 году читатели авторитетного математического журнала признали это уравнение «самой красивой математической формулой в истории математики».

Все эти изыскания в области истории расчета и применения числа π говорят о том, что даже сейчас, когда компьютеры выполняют многие математические расчеты, креативность человеческого ума всегда найдет себе выход. Применительно к количественному анализу в сфере бизнеса и корпораций компьютеры взяли на себя подавляющее большинство статистических расчетов. Но творчеству по-прежнему есть место там, где заходит речь об использовании этих расчетов для принятия решений.

Хотелось бы надеяться, что нам удалось показать читателям: аналитическое мышление и креативность не только вполне совместимы, но и тесно взаимосвязаны. Вы не сможете ни стать хорошим количественным аналитиком, ни компетентно пользоваться аналитическими данными, если не умеете подключать к делу все ваши творческие способности. Однако помните, что в манипулировании цифрами и интерпретации результатов анализа баз данных креативность должна иметь предел. Творческий подход очень важен, но правда еще важнее.

Профессор математики в Политехническом институте штата Джорджия Тед Хилл в начале курса дает студентам задание на дом: или подбросить монетку двести раз и записать результаты, или представить, как подбрасываешь монетку двести раз, и сфальсифицировать результаты. На следующем семинаре он просматривает отчеты о домашней работе и, к восторгу аудитории, легко обнаруживает почти всех, кто занимался фальсификациями. Как это ему удается? На основании небольшого эксперимента он знает, что в некоторый момент при длительном подбрасывании монетки начинают выходить серии из шести-семи орлов или решек подряд. «Фальсификаторы» об этом не знают и интуитивно пытаются не писать подряд слишком много одинаковых результатов, поскольку считают, что это маловероятно. Хилл с первого взгляда выявляет записи о шести-семи орлах или решках, выпавших подряд (или их отсутствие), на основе чего и делает вывод о действительно проведенном студентом эксперименте или о фальсификации его результатов. На первый взгляд, это просто небольшой фокус для привлечения внимания студентов, но на самом деле в этом есть глубокий смысл. Если в данных отсутствуют те модели и зависимости, которые вы ожидали там увидеть, логично предположить фальсификацию или мошенничество.

Мы хорошо знаем, что наша система исчисления использует цифры от 1 до 9. Поэтому можно предположить, что вероятность выбора любой из этих цифр в качестве первой значащей в числе равна 1/9. Но, как ни странно, это не так. «Закон первой цифры», называемый также законом Бенфорда, гласит, что в списке чисел, взятых из реальных баз данных, частота распределения той или иной цифры на первое место в числе подчиняется специфической закономерности: примерно в 30 процентах случаев такой цифрой будет 1, а вероятность появления на первом месте остальных цифр тем меньше, чем цифра больше [80]. В соответствии с законом Бенфорда вероятность распределения цифр на первом месте в числе такова:

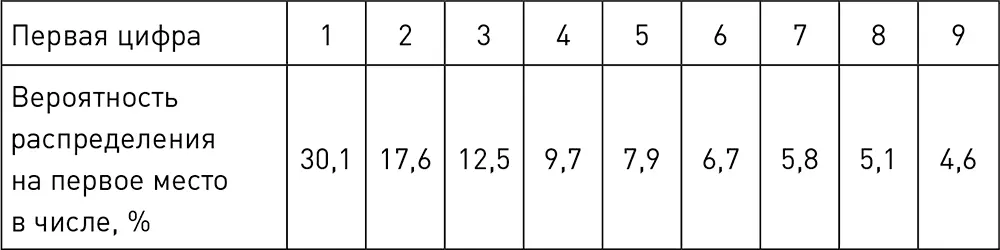
Этот довольно удивительный факт был обнаружен в 1881 году американским астрономом Симоном Ньюкомбом, заметившим, что в справочнике логарифмов первые страницы всегда гораздо более потрепанные, чем последующие. В 1938 году физик Франк Бенфорд сделал то же открытие на основе анализа гораздо большего массива данных, чем Ньюкомб. Он рассмотрел 20 229 наборов данных, включая географические координаты рек, бейсбольную статистику, количество статей в журналах, и номера домов первых 342 человек, перечисленных в рейтинге «Деятели науки Америки». Анализ всех этих вроде бы не связанных друг с другом баз данных показал, что вероятность распределения цифр на первое место в числе та же, что и для потрепанных таблиц логарифмов. Эта модель определения первой цифры в числе получила впоследствии название закона Бенфорда в честь ее первого исследователя. Стало общепризнанным действие закона Бенфорда во многих ситуациях реальной жизни.