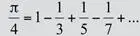Ким Хо - О чем говорят цифры. Как понимать и использовать данные

Обзор предшествующих исследованийПодобные исследования ранее практически не проводились. Единственное, что было известно, это то, что товары для малышей высокорентабельны, поэтому было бы хорошо найти товары, вместе с которыми они бы чаще продавались и, соответственно, рос бы их объем продаж.

Моделирование (отбор переменных). Частота покупок различных видов товара по данным кассовых аппаратов аптек.

Сбор данных. Osco Drug располагала данными с кассовых аппаратов в своих аптеках (розничных торговых точках) и предоставила их аналитикам. База данных содержала информацию о перечне и ценах купленных по одному чеку товаров по 1,2 миллиона таких чеков, пробитых в двадцати пяти аптеках сети.

Анализ данных. Сегодня доступны значительно более сложные технологии интеллектуального поиска данных, но в 1992 году они еще не получили распространения. Команда аналитиков Teradata сформулировала запросы по базе данных, чтобы выявить товары, покупаемые вместе чаще, чем другие. Такой анализ, проведенный К. Хис, одной из членов группы, показал, что покупатели (вообще говоря, не обязательно мужчины), заходившие в магазин в интервале между 17:00 и 19:00 по четвергам и субботам, очень часто покупали вместе пиво и пеленки. Однако никаких статистических тестов для подтверждения того, что это не случайное явление, проведено не было.

Результаты и необходимые меры. Это именно тот случай, когда анализ показал свою неэффективность. В досужих рассуждениях об этой истории частенько проскальзывали разные предположения – например, что магазинах пиво и пеленки располагались на соседних стеллажах или что, наоборот, они находились в разных концах магазина и покупателям приходилось пересекать весь торговый зал. По сути, ни одно из этих предположений не подтвердилось. Результат анализа сочли забавным курьезом, и ни аналитики Teradata, ни менеджеры Osco Drug даже не пытались произвести какие-то действия на их основе или хотя бы оценить потенциальные их последствия.

У нас недостаточно информации, чтобы судить о том, почему этот интересный пример поиска моделей в данных так и не получил достойного продолжения. Но он наглядно свидетельствует о том, что любой этап аналитического процесса будет эффективным только в том случае, если приведет к какому-то результату. Компьютеры способны найти модели в базе данных, но только человек может сказать, есть ли в этих моделях какой-то смысл, и принять соответствующие меры (см. вставки «Компьютеры и модели: число π» и «Закон первой цифры – способ обнаружения мошенничества»).

Число π – это отношение длины окружности к ее диаметру. π приблизительно равно 3,141592 в обычном десятичном исчислении. Многие формулы математики, инженерного дела и науки используют это значение, что и делает его самой важной математической концепцией после теоремы Пифагора [77].

π – иррациональное число, что означает, что его значение не может быть выражено обыкновенной дробью, а последовательность знаков после запятой никогда не заканчивается и не является периодической. Однако это не значит, что человечество, начиная с древних вавилонян и до современных математиков, прекратило попытки обнаружить повторяемость в десятичных знаках π.

Конечно, появление компьютеров в XX веке привело к новым попыткам поставить рекорд, рассчитав число π до еще большего количества знаков; компьютеры полностью заменили в этом деле людей. Нынешний рекорд количества разрядов, до которых рассчитано число π, составляет пять триллионов. Дальнейшее увеличение числа разрядов зависит не столько от математических способностей человека, сколько от технических возможностей компьютеров. Тем не менее до сих пор повторяющихся групп цифр в знаках числа π не обнаружено.

Зато математики нашли множество новых применений этому замечательному числу, что говорит о важной роли креативности в аналитическом мышлении. Например, математик Дэвид Ачесон рассказывает такую историю.

Представьте себе удивление математиков, когда в середине XVII века они обнаружили появление числа π в разных областях, подчас весьма далеких от геометрии окружности. Один из самых замечательных фактов этого рода состоит в необычной связи между π и рядом нечетных чисел.

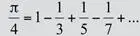
…Удивительные взаимосвязи такого рода принадлежат к явлениям, которые всегда волновали математиков» [78].