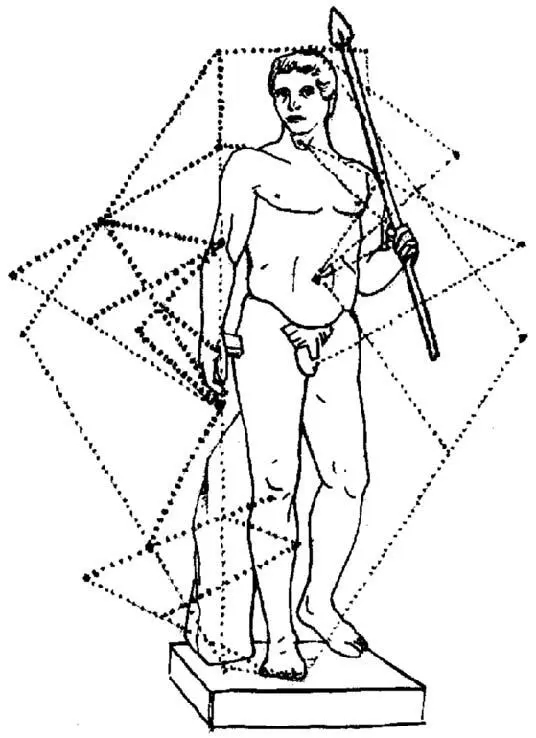
Пропорция золотого сечения в статуе Дорифора работы древнегреческого скульптора Поликлета
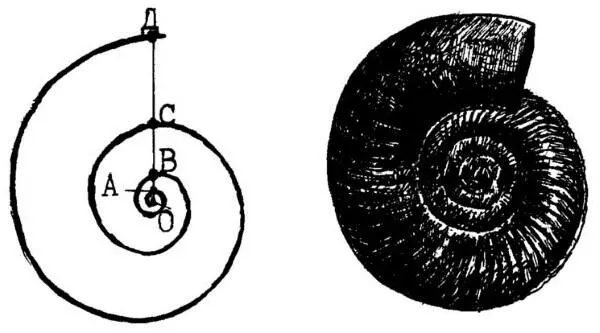
Соблюдение пропорций золотого сечения в математике и природе: слева – спираль, в которой наблюдается гармоничное сочетание отрезков, выраженное через отношение: ОВ: OB = OB: OC = OC: OД и т. д. Спарава – спиралеобразная раковина древнего моллюска, построенная им в соответствии с правилами золотого сечения
Если соотнести длину предплечья с длиной ладони, то получится пропорция фи, так же длина плеча относится к длине предплечья. Или отнесите длину голени к длине стопы и длину бедра к длине голени, и т. д. Пропорция фи обнаруживается во всей скелетной системе. Она обычно отмечается в тех местах, где что-то сгибается или меняет направление. Она также обнаруживается в отношениях размеров одних частей тела к другим. Изучая это, все время удивляешься.
На следующем рисунке представлен еще один способ демонстрации пропорции фи. Здесь кривые показаны таким образом, что видно, как одна кривая связана с другой; вы видите целый каскад пропорций фи в человеческом теле…
…Греки хорошо понимали пропорцию фи. Так же, как египтяне и многие, многие другие древние народы. Когда они создавали произведение искусства. они проводили измерения, чтобы убедиться в том, что математически все точно соответствует пропорции фи… Они могли придать лицу любое выражение или создать статую, выражающую любое чувство. Греки творили, соединяя левое и правое полушария.
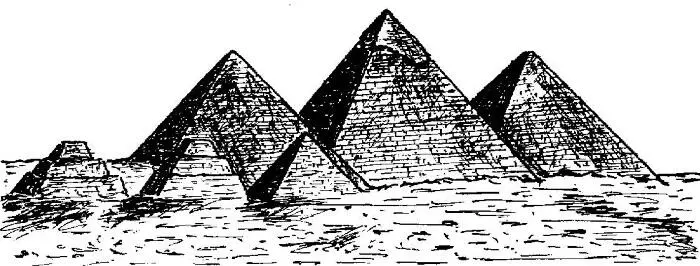
Великие пирамиды Хеопса, Хефрена и Микерина
Когда римляне одержали верх над Грецией, они абсолютно ничего не знали о сакральной геометрии. Они видели невероятно высокое греческое искусство и пытались подражать ему, но если вы сравните греческое и римское искусство после завоевания Греции, то римское искусство выглядит как любительское. И хотя римские художники были действительно искусны в том, что делали, они просто не знали, что необходимо было измерять все, – требовалось именно это совершенство, чтобы тело выглядело настоящим».
В разных стилях классической архитектуры в мире использовали те же принципы. Парфенон в Греции выглядит совершенно иначе, чем японская пагода, но воплощает ту же математику. А Великая Пирамида выглядит совсем не так, как каждое из этих двух зданий, но и она воплощает ту же математику.
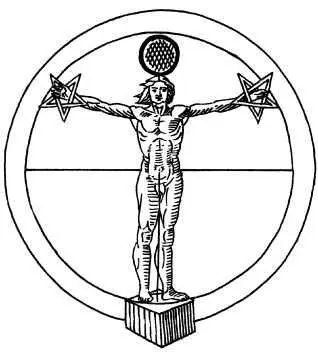
Геометрические символы [10] Айванхов О. М. Язык геометрических фигур; Бауэр В. и др. Энциклопедия символов; Гудман Ф. Магические символы; Купер Дж. Энциклопедия символов; Рудникова Н. П. Сокровенная мудрость Египта: Солнечный путь. Арканы Таро; Фрисселл Б. В этой книге нет ни слова правды, но именно так все и происходит.
Абсолютный символический язык – это язык геометрических фигур…
Геометрические фигуры – конкретное воплощение чисел. Числа принадлежат к миру принципов, и они становятся геометрическими фигурами, спускаясь в физический план.
О. М. Айванхов
Простейшие геометрические символы
Когда Посвященные прошлого рисовали вертикальную или горизонтальную линию, круг или точку, а затем комбинировали из них крест, треугольник, квадрат, пентаграмму, гексаграмму или змею, кусающую свой хвост… они вкладывали в каждую фигуру вечные знания.
О. М. Айванхов
Практически все геометрические символы состоят из комбинаций нескольких геометрических элементов – простых составных частей, каждая из которых имеет в то же время свое особенное значение, внося свой вклад в общую композицию.
Наиболее простыми из таких магических «частичек»-символов являются точка, круг, разновидности дуг, образованные из круга, вертикальная и горизонтальная линии, а также треугольник, квадрат или прямоугольник.
На самом деле значения этих, казалось бы, простых фигур достаточно сложны.
В мистических представлениях точка – символ центра, источник жизни, символ первичной созидательной энергии, которую иногда представляют настолько сконцентрированной, что отражать ее может лишь нечто нематериальное, например отверстие. Древний символизм точки как предельно сжатой энергии, широко распространенный в мистической литературе, чрезвычайно близок к современным физическим и астрономическим теориям о происхождении Вселенной.
Читать дальше
















