Друнвало Мельхиседек - Древняя Тайна Цветка Жизни. Том 2

В каждом круге пять равных частей. Единственная проблема была в том, что это построение не годилось, оно не работало. Я не мог в это поверить! Я-то думал, что все будет так просто и отсюда я пойду дальше, но ничего не получалось. Это построение не работало геометрически. Тогда я вернулся назад и проверил оба рисунка, уверенный, что не мог ошибиться. Оно там, это же ясно как день. Но когда я снова их соединил, они опять-таки не совмещались.

После многих-многих часов бесплодных попыток я вернулся к тому, с чего начал, и принялся заново изучать исходный рисунок Люси. Определенно, в среднем круге было пять делений и по семь делений с каждой его стороны. Потом я раздобыл специальный небольшой прибор для измерения размера ступенек лестницы. Оказалось, что семь делений под и семь делений над центральным кругом были меньше тех, что находились внутри него! Люси изменила размеры, чтобы они подходили! Она знала , что мы находимся на негармоничном уровне сознания; она знала, что лестница не впишется, если не изменить некие параметры, но хотела все это поместить в одном рисунке. Поэтому она заставила лестницу вписаться, зная, что если люди исследуют ее, то поймут, что уровень с 19 делениями, который она нарисовала, является негармоничным уровнем сознания.

Это был тонкий подход, подобный тому, как в каноне человека, в верхней части своего рисунка, Леонардо сделал надпись в зеркальном отражении, чтобы вам пришлось держать зеркало для ее прочтения. Точно так же исходный рисунок Люси – это мужской аспект, а его женской составляющей является зеркальное отражение. Это как бы небольшая игра по сокрытию того, что вы не хотите сообщать внешнему миру. Словно внезапно прозрев, я и впрямь стал понимать, что наш уровень сознания действительно дисгармоничный, и египтяне тоже это знали. С той поры я стал намного больше времени проводить за изучением рисунков Люси.

Теперь, зная, что египтянам были известны три уровня сознания, мы вернемся к тем трем геометрическим рисункам и тщательно их изучим. Это линзы, которыми пользуется каждый уровень человеческого сознания для интерпретации Реальности: 8 на 10, 10 на 12 и 14 на 18. Начнем с прорисовки 8 на 10, первого уровня сознания.

Тот показал мне гениальный способ построения этого рисунка без замеров и расчетов. Вам нужны лишь линейка и циркуль. Он сам показал мне, как это делается, сказав, что данный метод сбережет массу времени (см. инструкции к рис. 9.15 под ним).

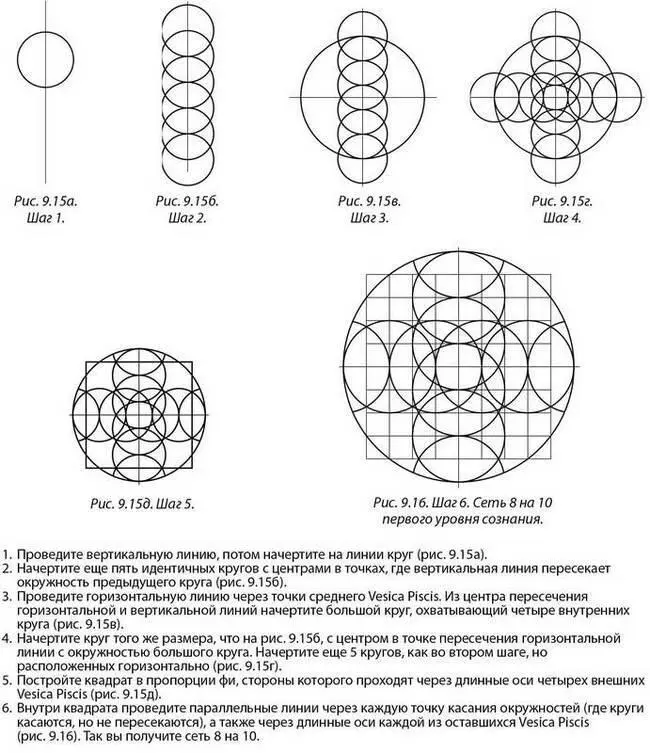
Закончив последний шаг, вы имеете сеть из 64 квадратиков в большом квадрате и большой круг, выходящий за периметр большого квадрата ровно на одну ширину квадратика (рис. 9.16). Большой квадрат в поперечнике составляет 8 квадратиков, а большой круг – 10 квадратиков: идеальные 8 на 10. И вам не нужна линейка!

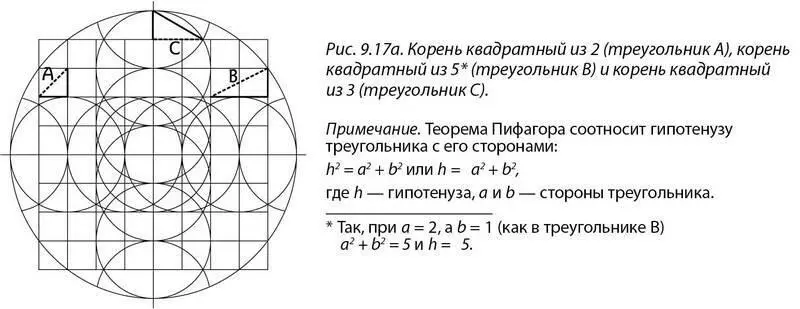
Есть и другой аспект сети 8 на 10, но пока я коснусь его лишь слегка. Может быть, кто-то из вас знает, что всю свою философию египтяне свели к корню квадратному из 2, корню квадратному из 3, корню квадратному из 5 и треугольнику 3–4–5. Феноменально, но все эти составляющие есть в рисунке первого уровня сознания. Если длину стороны квадратиков на рисунке 9.17а принять за 1, то диагональ А равна корню квадратному из 2; диагональ В равна корню квадратному из 5; а линия С – корню квадратному из 3, из равностороннего треугольника Vesica Piscis.

Например, под квадратным корнем из пяти я подразумеваю, что если четыре квадратика принять за единицу (рис. 9.17б), то линия D будет равна 1, а линия Е = 2.

Теорема Пифагора утверждает, что диагональ (гипотенуза) прямоугольного треугольника равна корню квадратному из суммы квадратов его катетов. То есть 12 = 1; 22 = 4; затем 1+ 4 = 5, образуя диагональ корня квадратного из 5. Вот что имеется в виду под корнем квадратным из 5. Посмотрите на рисунок 9.17б, где четыре квадратика равны единице.

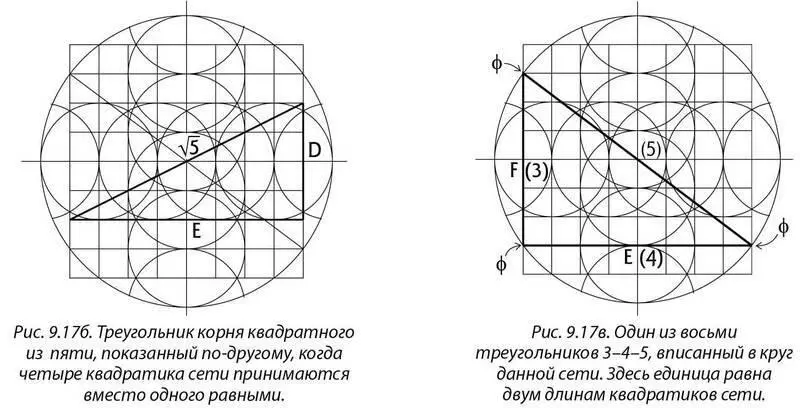
Треугольник 3–4–5 прекрасно вписывается в рисунок 9.17 в. Если длину двух квадратиков принять за единичный отрезок, то линия F равна 3 отрезкам (6 квадратикам), а линия Е – 4 отрезкам (8 квадратикам). Так как стороны треугольника равны 3 и 4, то диагональ должна быть равна 5, следовательно, образуется треугольник со сторонами 3–4–5. На самом деле их 8, идеально вписанных в эту фигуру и закручивающихся вокруг ее центра. Но самое невероятное – треугольники 3–4–5 точно вписаны в круг, касаясь тех его точек, где круг пересекает квадрат, образуя пропорцию фи . Это удивительная синхронизация, которая не может произойти в результате простого совпадения.