Друнвало Мельхиседек - Древняя Тайна Цветка Жизни. Том 2

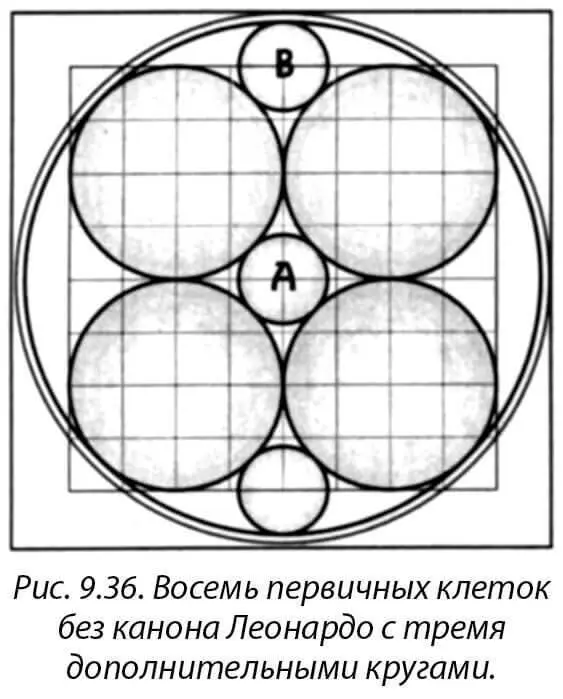
Это двухмерное изображение восьми первичных клеток. А в трехмерной форме, если бы вам надо было поместить в середину сферу, то она, словно мраморный шарик, проскользнула бы дальше к центру, лишь коснувшись больших сфер. Такая сфера представлена кругом в точке А. Если вы возьмете круг того же размера и поместите его сверху (В), он только коснется внутренней поверхности блестящей оболочки, показывая вам ее расположение.

Затем возьмите круг несколько большего размера, помещающийся позади меньшего круга в центре и вписывающийся в 64-клеточную сеть (см. рис. 9.36а). Если вы поместите такой круг в точку В, он вам точно покажет внешнюю поверхность блестящей оболочки. Итак, меньший круг, коснувшийся сфер, и другой, побольше, точно поместившийся внутри, – это ключи к внутренней и внешней поверхности блестящей оболочки. Они показывают, как эти элементы соотносятся в пропорции фи . Мне известен только этот способ расчета, хотя, быть может, есть и другие способы.

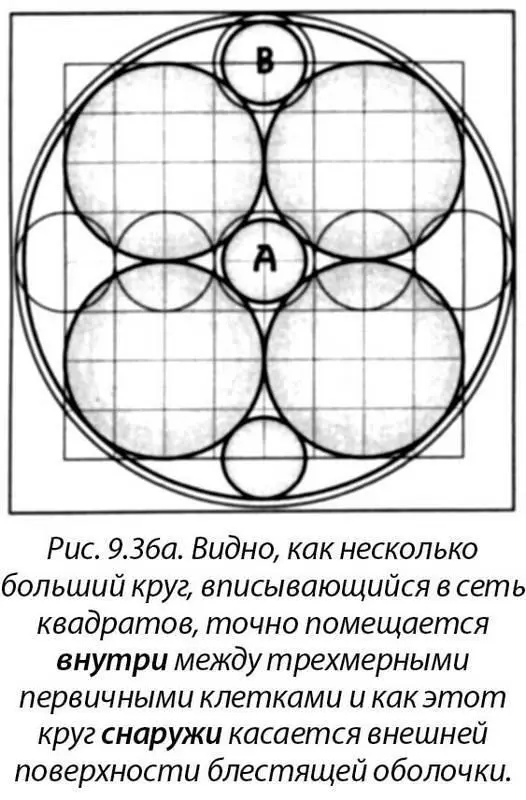
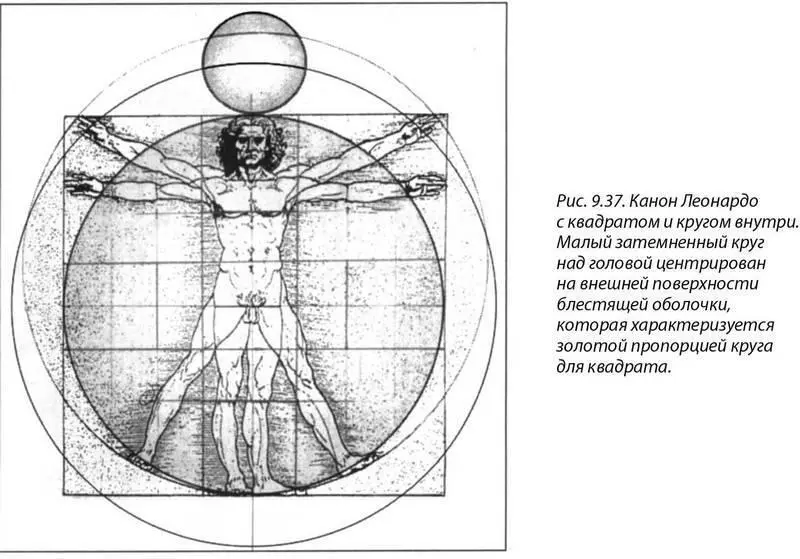
А теперь вернемся к рисунку Леонардо, наложенному на восемь первичных клеток. На рисунке 9.37 мы налагаем на канон да Винчи другую геометрию, отображающую его дальнейшую связь с макрокосмом, а также с микрокосмом. Взгляните на большую темную сферу, точно описывающую тело человека от головы до ступней, ту, что внутри квадрата с телом. Затем посмотрите на меньший затемненный круг прямо над головой человека. Этот круг получается, если иголка циркуля помещена в верхнюю точку круга пропорции фи с телом человека, а грифель циркуля касается макушки головы. Тот же круг на рисунке 9.35 имел бы радиус от внешней поверхности блестящей оболочки до макушки головы или квадрата. Меньший круг лишь касается большего темного круга. (Побочное замечание: центр меньшего круга находится точно в месте расположения тринадцатой чакры.)

И что все это значит?

Многие люди заявляли о своем праве считаться первоисточником приводимой ниже информации, но ни один из них не был ее истинным источником, потому что я нашел человека, который занимался этим еще раньше, и от него, видимо, все исходило. Самой ранней из всех работ, что я смог найти, была книга «Ритмы Видения» Лоуренса Блэра ( Rhythms of Vision, by Lawrence Blair), но он не претендует на первенство, говоря, что нашел эту информацию в более ранних работах. Я не знаю, кто первый пришел к этой идее, но она действительно поразительная, особенно если вы раньше о ней не слышали.

Подумайте: размеры двух затемненных сфер на этом рисунке (рис. 9.37) «случайно» имеют точно такую же пропорцию, что и Земля с Луной. Та же пропорция есть в человеческом теле и в первичных восьми клетках всех форм жизни. Кроме того, не только сферы на этом рисунке обладают такими же относительными размерами, как и Земля с Луной, – квадрат, который описал бы Землю, и круг, который простерся бы до центра Луны, соприкасайся она с Землей, тоже имели бы пропорцию фи . Это вполне убедительно подтверждает соотношение размеров Земли и Луны.

Для доказательства вам надо знать диаметр Земли, равный стороне описывающего ее квадрата, подобного тому, в который вписано человеческое тело. Сначала нужно вычислить, сколько миль потребуется, чтобы обойти Землю по квадрату; для этого умножьте диаметр на 4. Затем следует узнать, сколько миль придется идти по кругу, простирающемуся до центра Луны, если бы Луна соприкасалась с Землей.

Давайте посмотрим, что у нас получилось.

Средний диаметр Земли 12 750 км, средний диаметр Луны 3477 км. Периметр квадрата, в который вписалась бы Земля, равен диаметру Земли, умноженному на 4, то есть 51 000 км. Для вычисления окружности круга, простирающегося до центра Луны, вам надо знать радиус Земли и радиус Луны, как верхней, так и нижней фигур рисунка 9.37, то есть сумму диаметров Земли и Луны, умноженную на π. Если эти числа будут равны или очень близки, то искомое будет доказано. Длина окружности круга равна диаметру Земли 12 750 км плюс диаметр Луны 3477 км, что равно 16 227 км. Умножив это число на π (3,1416), получим 50 979 км (см. рис. 9.38) – разница всего в 21 км! Учитывая, что на экваторе океан на 43 км выше, чем где-либо еще (океан вытянут в 43-километровый гребень), 21 км ничего не значит. Однако если вы умножите 16 227 км на 22/7 (это число часто применяется при расчетах как наиболее близкое к π), то получите точно такое же число , как и периметр квадрата, – почти 51 000 км!