Даниил Шибаев - Вечный завет или Откровение в стиле рок

Конечно чистота эксперимента затруднительна в виду отсутствия материала позволяющего шару растягиваться от нулевых значений, но думаю поправки к этому ни у кого не вызовут недоумения.

ПОЛОЖЕНИЕ 2:

Функция обладает телом, которое стремиться принять форму наиболее эргономичного ее существования, либо, при заданных условиях, совершить работу с максимальной отдачей. Размеры тела функции зависят от количества, задействованного в ней, импульса в первообразном виде или количества импульсных систем, с суммарным импульсом, являющихся ее составными частями

А причем тут рок-н-ролл, спросят некоторые. Ведь наш глаз вроде бы не врет, показывая, что волны на воде распространяются радиально. Вроде бы так, но тот же глаз нам показывает, что все задействованное в той же солнечной системе имеет орбитальную скорость. Вроде бы что тут такого. Можно ведь объяснить и магнитными полями и еще бог, или черт знает чем. А нужно ли? Коль рубанули Оккамовым инструментом, так рубанули начисто. Никаких нам структурных составляющих не надо и посему добавим еще одно положение.

ПОЛОЖЕНИЕ 3:

Волны, распространяющиеся внутри системы от источника колебаний, распространяясь от него, одновременно обладают моментом вращения, который определяет и вращение самой функции

Правильно, зачем нам разбрасываться на два вращения, будем эргономичными, раз вращается что-то одно, значит, вращается и все в единой системе. Ну а на примере солнечной системы любой астроном сможет рассчитать все параметры этой задачи, выводя систему зависимостей между количеством импульса, скоростью распространения волн и их угловой скоростью зависящей от удаленности от источника. Тут уж не поспоришь, инертность есть инертность, даже если это инертность движения, а не покоя.

Импульс начала, мяч в игре,

Итак, исходя из предыдущей главы, мы внесем лишь небольшую деталь к цитате Вавилова — мир покоится на инерции вращения взамен укоренившейся инерции прямолинейного движения. Функция и не могла проявить себя иначе, разделяясь на кучу ее составляющих, по определению современной науки, структур. Тут мы получаем подобие шарика из нашего опыта, где под воздействием вращения его стенки сами стараются расправиться. Впрочем, все станет ясней дальше. А пока продолжим нашу историю.

Лиха беда — начало.

Итак, наше ничто начало крутиться. Появилась ось вращения. По мере наращивания скорости и растяжения начали происходить и другие изменения. Вначале они насторожили, поскольку были новы и необычны. Дело в том, что попытавшись заглянуть за свои границы, наше нечто слегка вытянулось. Попытка, конечно, была обречена на провал, но зато получился интересный эффект который невозможно было заметить когда вращаясь оно принимало форму сбалансированного идеального круга. На что это походило?

Порой на уроках физики демонстрировался опыт. Через подвешенную проволочную рамку пропускали ток. И как следствие этого тока рамка начинала скручиваться.

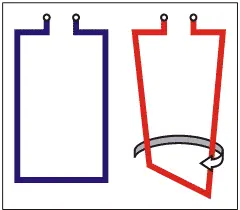
Так вот, как только появилось небольшое смещение, как тут же началось и изменение состояния. Впору было испугаться, но для нечто , которого уже утомило в предвечности состояние мертвой стабильности, был даже рад. Тем самым заложив еще один принцип для дальнейшего развития вселенной. Принцип заключался в том, что в нашем мире нашло наиболее полное отображение в авиастроении как в системе создания неустойчивых аэродинамических схем наделяющих систему максимальной свободой маневра.

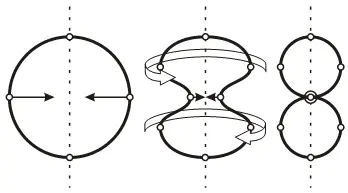
Еще раз пусть простят меня ученые за несоблюдение пропорций, право, я не настолько владею графическими инструментами и мне проще рисовать окружностями и прямыми. И коль на то пошло, то именно вашей очередной задачей будет определение всех точек эксцентриситета для любой системы подчиненной нашему принципу.

Но что произошло когда вращение достигло того значения когда импульсная система обрела свое проявление в новом для нее виде? Хотя в новом ли? Почти все атрибуты были те же за исключением того что она как бы раздвоилась. Из четырех базовых точек, две из которых были осевыми, а две стремящимися друг к другу частями при скручивании, получилось семь. Правда одна была как бы двойной.